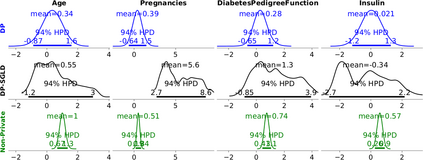
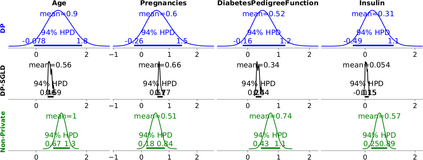
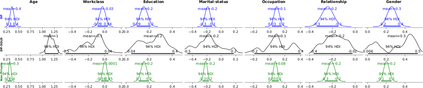
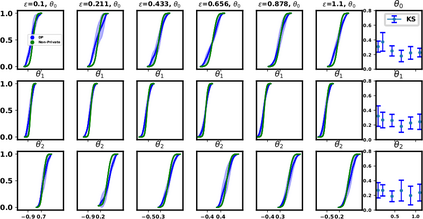
Generalized linear models (GLMs) such as logistic regression are among the most widely used arms in data analyst's repertoire and often used on sensitive datasets. A large body of prior works that investigate GLMs under differential privacy (DP) constraints provide only private point estimates of the regression coefficients, and are not able to quantify parameter uncertainty. In this work, with logistic and Poisson regression as running examples, we introduce a generic noise-aware DP Bayesian inference method for a GLM at hand, given a noisy sum of summary statistics. Quantifying uncertainty allows us to determine which of the regression coefficients are statistically significantly different from zero. We provide a previously unknown tight privacy analysis and experimentally demonstrate that the posteriors obtained from our model, while adhering to strong privacy guarantees, are close to the non-private posteriors.
翻译:诸如后勤回归等一般线性模型(GLMs)是数据分析员档案中最广泛使用的武器之一,并经常用于敏感数据集。大量以前在有区别隐私限制的情况下调查GLMs的大量先前工作只提供对回归系数的私人点估计,无法量化参数不确定性。在这项工作中,以后勤和Poisson回归为例,我们采用通用的有噪音觉悟的DP Bayesian推理方法,目前掌握的GLM方法,因为摘要统计数据之和杂乱不宁。量化不确定性使我们能够确定哪些回归系数在统计上与零有很大不同。我们提供了以前未知的严密隐私分析,并实验性地证明,从我们模型中获得的后方虽然坚持严格的隐私保障,但接近非私人后方。