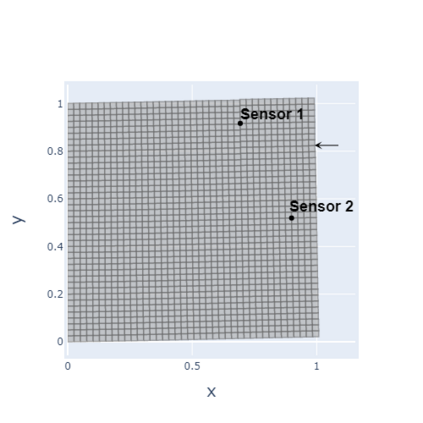
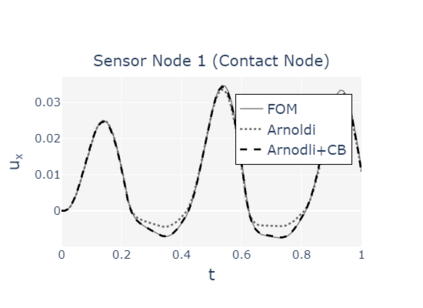
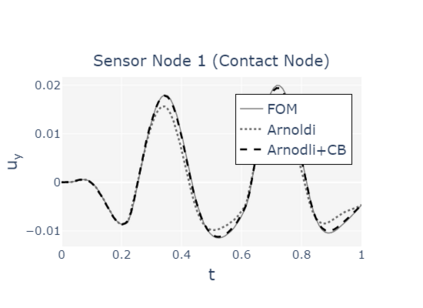
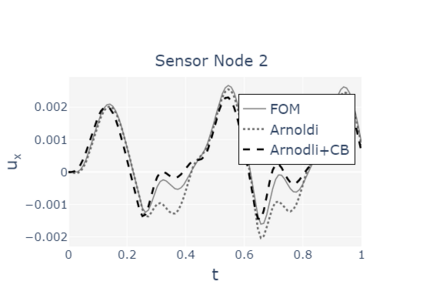
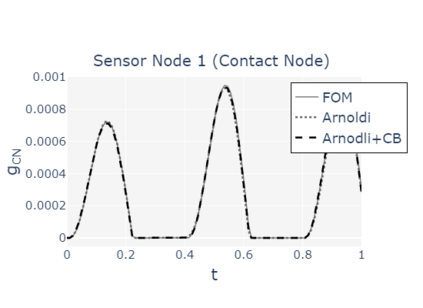
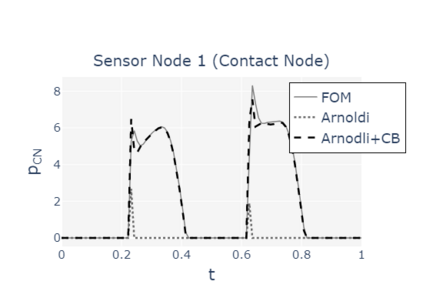
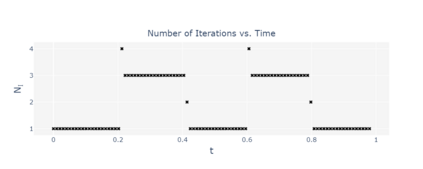
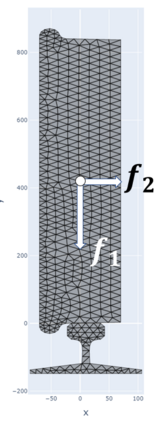
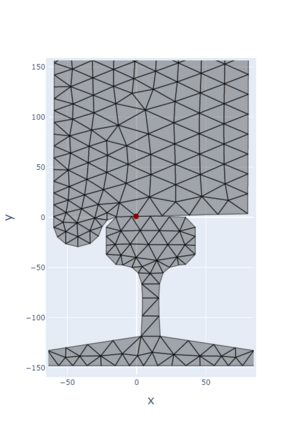
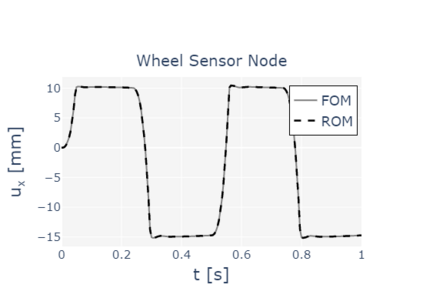
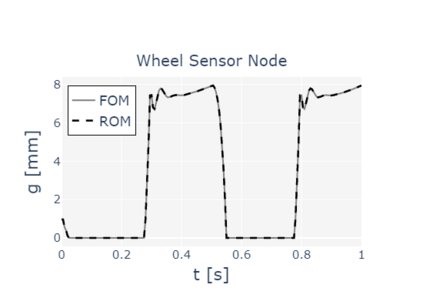
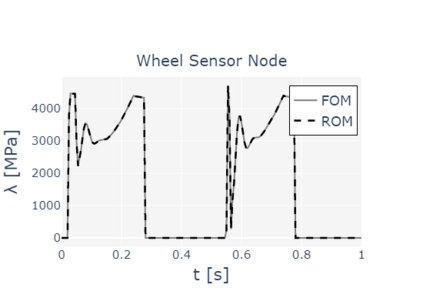
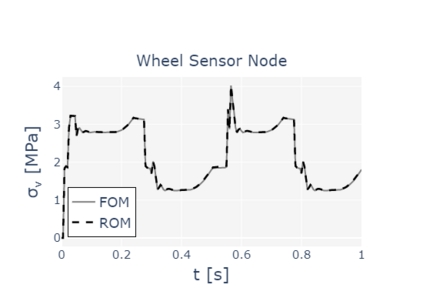
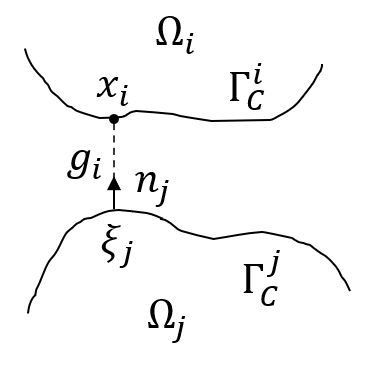
The paper presents a new reduction method designed for dynamic contact problems. Recently, we have proposed an efficient reduction scheme for the node-to-node formulation, that leads to Linear Complementarity Problems (LCP). Here, we enhance the underlying contact problem to a node-to-segment formulation. Due to the application of the dual approach, a Nonlinear Complementarity Problem (NCP) is obtained, where the node-to-segment condition is described by a quadratic inequality and is approximated by a sequence of LCPs in each time step. These steps are performed in a reduced approximation space, while the contact treatment itself can be achieved by the Craig-Bampton method, which preserves the Lagrange multipliers and the nodal displacements at the contact zone. We think, that if the contact area is small compared to the overall structure, the reduction scheme performs very efficiently, since the contact shape is entirely recovered. The performance of the resulting reduction method is assessed on two 2D computational examples
翻译:本文为动态接触问题提出了一种新的减少方法。最近,我们为节点到节点的配方提出了一个有效的削减计划,这导致了线性互补问题。在这里,我们将潜在的接触问题提升为节点到分的配方。由于采用了双重方法,获得了非线性互补问题,节点到分的状态被四面形不平等描述,每个步骤的顺序都接近于一次长点。这些步骤是在一个缩小的近似空间中实施的,而接触处理本身可以通过克雷格-班普敦方法实现,该方法保留了接触区域的拉格朗乘数和节点置换。我们认为,如果接触区域小于整个结构,则削减计划效果非常有效,因为接触形状完全恢复了。因此产生的削减方法的绩效根据两个2D的计算实例进行评估。