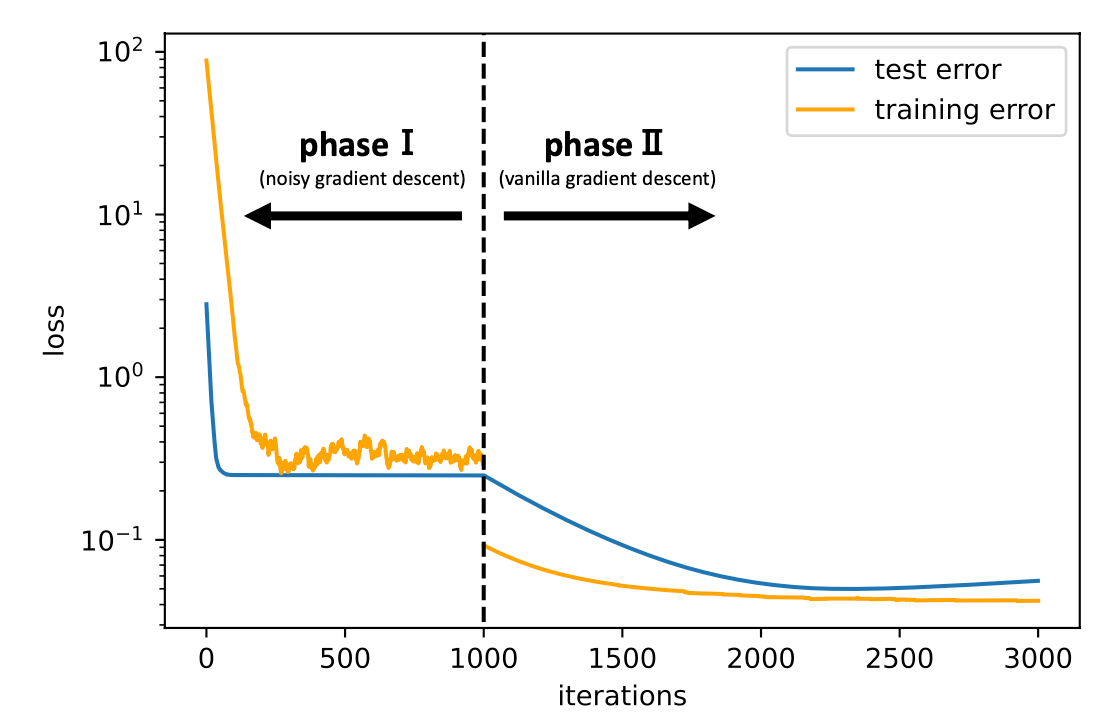
While deep learning has outperformed other methods for various tasks, theoretical frameworks that explain its reason have not been fully established. To address this issue, we investigate the excess risk of two-layer ReLU neural networks in a teacher-student regression model, in which a student network learns an unknown teacher network through its outputs. Especially, we consider the student network that has the same width as the teacher network and is trained in two phases: first by noisy gradient descent and then by the vanilla gradient descent. Our result shows that the student network provably reaches a near-global optimal solution and outperforms any kernel methods estimator (more generally, linear estimators), including neural tangent kernel approach, random feature model, and other kernel methods, in a sense of the minimax optimal rate. The key concept inducing this superiority is the non-convexity of the neural network models. Even though the loss landscape is highly non-convex, the student network adaptively learns the teacher neurons.
翻译:虽然深层次学习的成绩超过了其他各种任务的方法,但解释其原因的理论框架尚未完全建立。为了解决这一问题,我们调查了师生回归模型中两层RELU神经网络的超风险,在这个模型中,学生网络通过其产出学习了未知的教师网络。特别是,我们认为,学生网络的宽度与教师网络相同,分两个阶段培训:先是吵闹的梯度下降,然后是香草梯度下降。我们的结果显示,学生网络可以接近全球最佳解决方案,并超越任何内核方法估计器(更一般而言,线性估计器),包括神经红内核方法、随机特征模型和其他内核方法,从微缩成轴最佳速度的意义上说。造成这种优势的关键概念是神经网络模型的非凝固性。尽管损失环境高度非凝固,但学生网络适应性地学习了教师神经。