Universal Joint Approximation of Manifolds and Densities by Simple Injective Flows

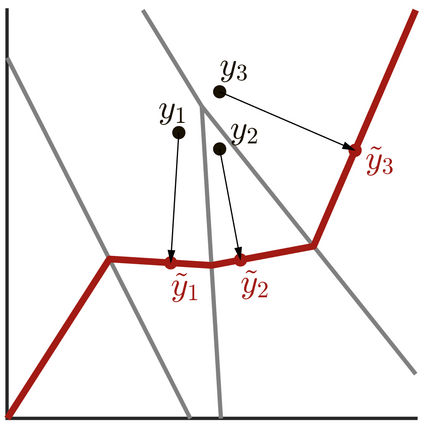
We study approximation of probability measures supported on $n$-dimensional manifolds embedded in $\mathbb{R}^m$ by injective flows -- neural networks composed of invertible flows and injective layers. We show that in general, injective flows between $\mathbb{R}^n$ and $\mathbb{R}^m$ universally approximate measures supported on images of extendable embeddings, which are a subset of standard embeddings: when the embedding dimension m is small, topological obstructions may preclude certain manifolds as admissible targets. When the embedding dimension is sufficiently large, $m \ge 3n+1$, we use an argument from algebraic topology known as the clean trick to prove that the topological obstructions vanish and injective flows universally approximate any differentiable embedding. Along the way we show that the studied injective flows admit efficient projections on the range, and that their optimality can be established "in reverse," resolving a conjecture made in Brehmer and Cranmer 2020.