Sampling-based multi-agent choreography planning: a metric space approach

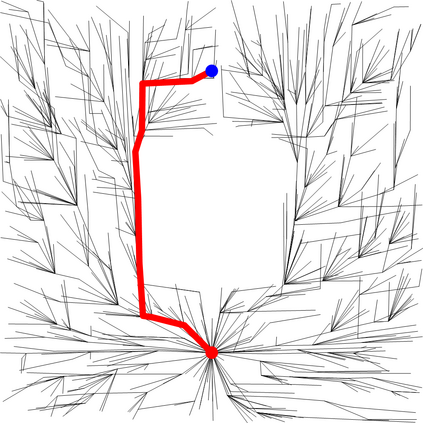
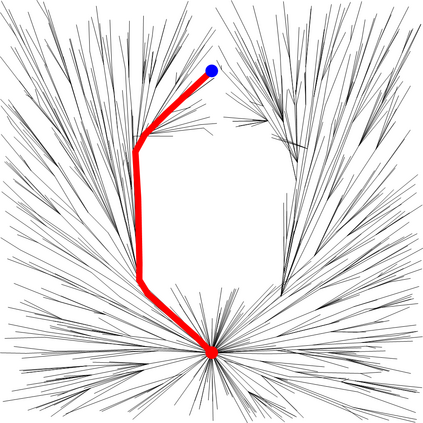
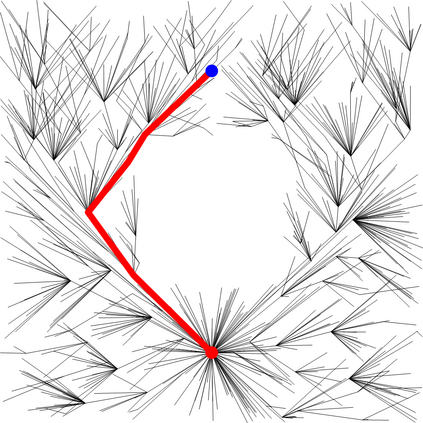
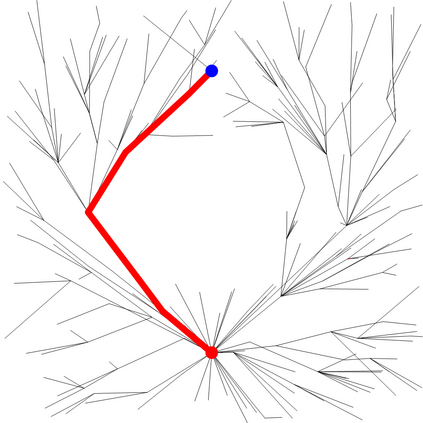
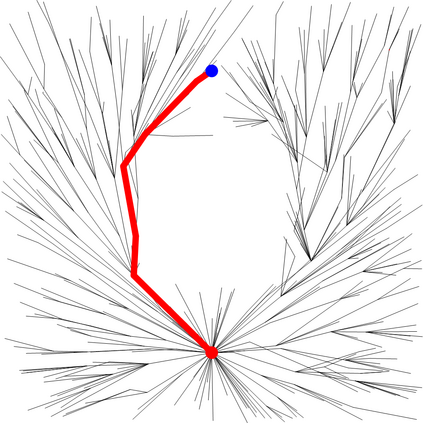
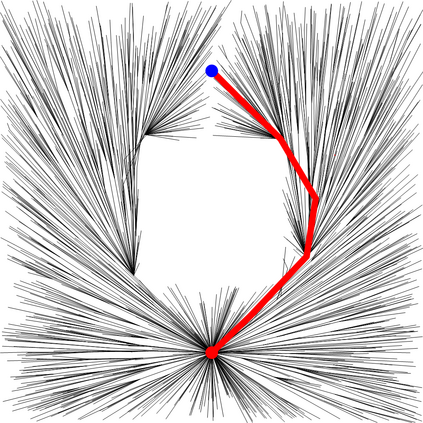
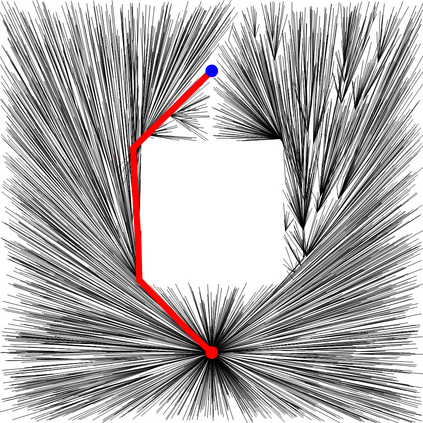
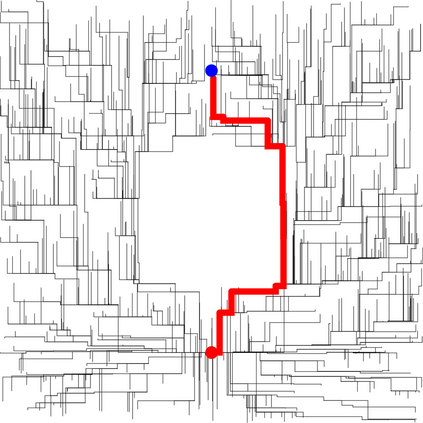
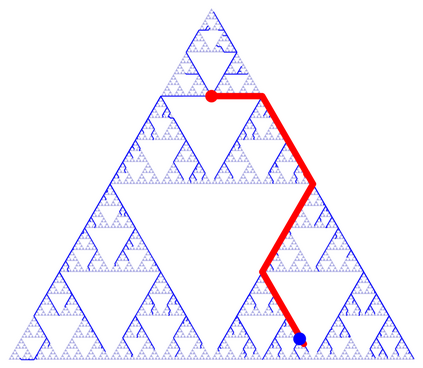
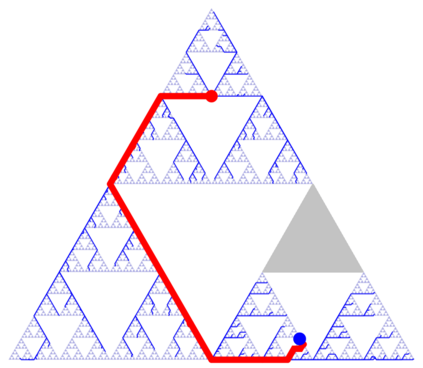
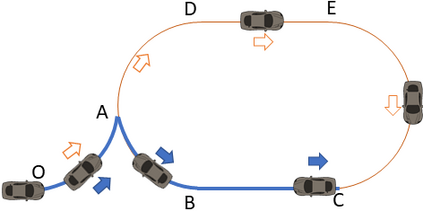
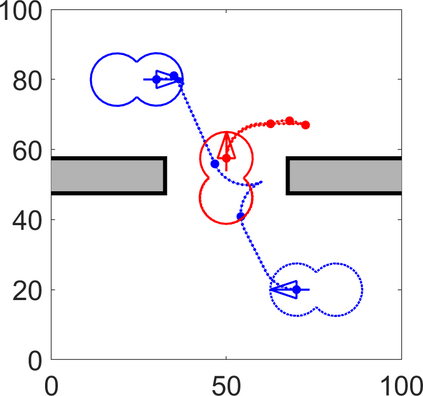
We present a metric space approach for high-dimensional sample-based trajectory planning. Sample-based methods such as RRT and its variants have been widely used in robotic applications and beyond, but the convergence of such methods is known only for the specific cases of holonomic systems and sub-Riemannian non-holonomic systems. Here, we present a more general theory using a metric-based approach and prove the algorithm's convergence for Euclidean and non-Euclidean spaces. The extended convergence theory is valid for joint planning of multiple heterogeneous holonomic or non-holonomic agents in a crowded environment in the presence of obstacles. We demonstrate the method both using abstract metric spaces ($ell^p$ geometries and fractal Sierpinski gasket) and using a multi-vehicle Reeds-Shepp vehicle system. For multi-vehicle systems, the degree of simultaneous motion can be adjusted by varying t.he metric on the joint state space, and we demonstrate the effects of this choice on the resulting choreographies.