Convergence under Lipschitz smoothness of ease-controlled Random Reshuffling gradient Algorithms

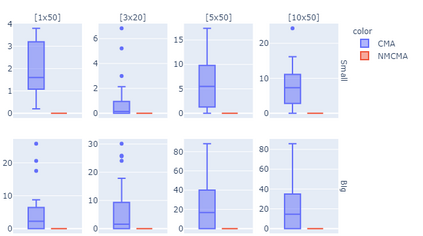
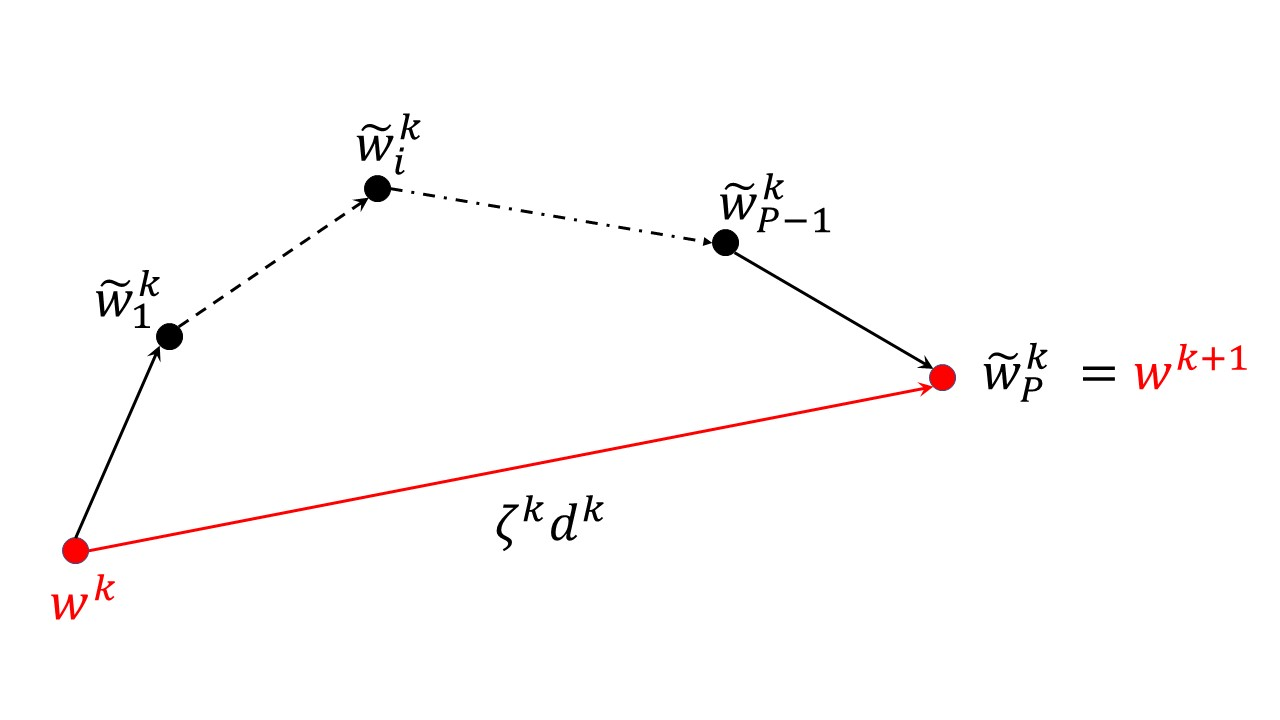
We consider minimizing the average of a very large number of smooth and possibly non-convex functions. This optimization problem has deserved much attention in the past years due to the many applications in different fields, the most challenging being training Machine Learning models. Widely used approaches for solving this problem are mini-batch gradient methods which, at each iteration, update the decision vector moving along the gradient of a mini-batch of the component functions. We consider the Incremental Gradient (IG) and the Random reshuffling (RR) methods which proceed in cycles, picking batches in a fixed order or by reshuffling the order after each epoch. Convergence properties of these schemes have been proved under different assumptions, usually quite strong. We aim to define ease-controlled modifications of the IG/RR schemes, which require a light additional computational effort and can be proved to converge under very weak and standard assumptions. In particular, we define two algorithmic schemes, monotone or non-monotone, in which the IG/RR iteration is controlled by using a watchdog rule and a derivative-free line search that activates only sporadically to guarantee convergence. The two schemes also allow controlling the updating of the stepsize used in the main IG/RR iteration, avoiding the use of preset rules. We prove convergence under the lonely assumption of Lipschitz continuity of the gradients of the component functions and perform extensive computational analysis using Deep Neural Architectures and a benchmark of datasets. We compare our implementation with both full batch gradient methods and online standard implementation of IG/RR methods, proving that the computational effort is comparable with the corresponding online methods and that the control on the learning rate may allow faster decrease.