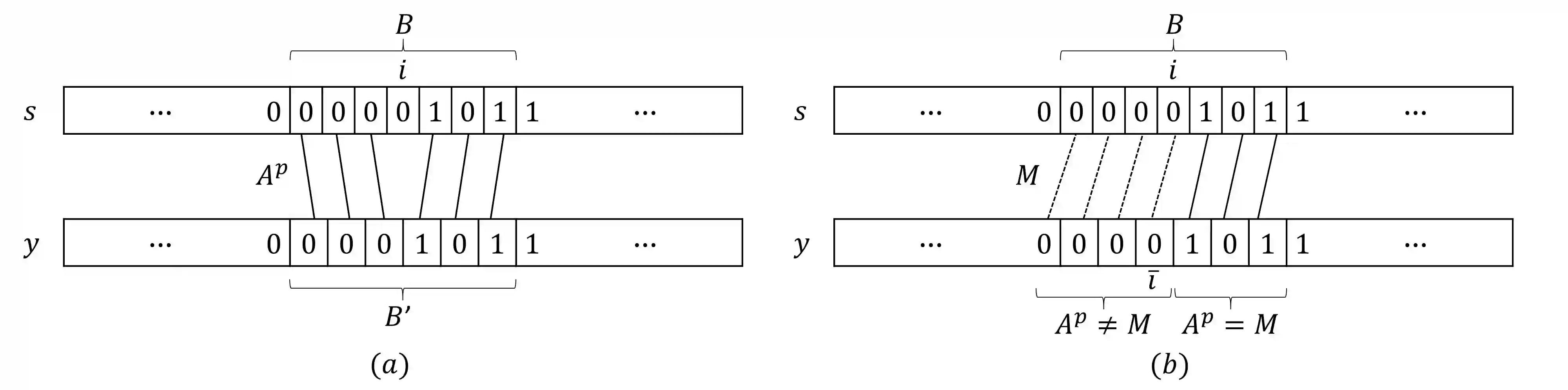
We consider an \emph{approximate} version of the trace reconstruction problem, where the goal is to recover an unknown string $s\in\{0,1\}^n$ from $m$ traces (each trace is generated independently by passing $s$ through a probabilistic insertion-deletion channel with rate $p$). We present a deterministic near-linear time algorithm for the average-case model, where $s$ is random, that uses only \emph{three} traces. It runs in near-linear time $\tilde O(n)$ and with high probability reports a string within edit distance $O(\epsilon p n)$ from $s$ for $\epsilon=\tilde O(p)$, which significantly improves over the straightforward bound of $O(pn)$. Technically, our algorithm computes a $(1+\epsilon)$-approximate median of the three input traces. To prove its correctness, our probabilistic analysis shows that an approximate median is indeed close to the unknown $s$. To achieve a near-linear time bound, we have to bypass the well-known dynamic programming algorithm that computes an optimal median in time $O(n^3)$.
翻译:我们考虑的是微量重建问题的 emph{ 近似} 版本, 目标是从美元追踪中回收一个未知的字符串 $s\ in ⁇ 0, 1 ⁇ n 美元( 每一个痕迹都是通过以美元计价的概率插入- 删除频道通过美元独立传递美元, 以美元计价) 。 我们为平均情况模型提出了一个确定性的近线时间算法, 美元是随机的, 仅使用 emph{ 3} 微量。 它运行在近线时间 $\ tilde O (n) 美元, 并且极有可能报告一个字符串在以美元计价( epsilon p n) 以美元计价编辑美元( $\ epsilon p n ) 内。 我们用一个精确的算法计算出三个输入微量中值的 $(1 ⁇ epsilon) 。 为了证明其正确性, 我们的精确性分析显示一个近于未知的中值中值 $ 。 要达到一个最接近于最精确的动态的平流的轨道 。