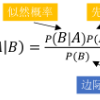
With the increasing intelligence and integration, a great number of two-valued variables (generally stored in the form of 0 or 1 value) often exist in large-scale industrial processes. However, these variables cannot be effectively handled by traditional monitoring methods such as LDA, PCA and PLS. Recently, a mixed hidden naive Bayesian model (MHNBM) is developed for the first time to utilize both two-valued and continuous variables for abnormality monitoring. Although MHNBM is effective, it still has some shortcomings that need to be improved. For MHNBM, the variables with greater correlation to other variables have greater weights, which cannot guarantee greater weights are assigned to the more discriminating variables. In addition, the conditional probability must be computed based on the historical data. When the training data is scarce, the conditional probability between continuous variables tends to be uniformly distributed, which affects the performance of MHNBM. Here a novel feature weighted mixed naive Bayes model (FWMNBM) is developed to overcome the above shortcomings. For FWMNBM, the variables that are more correlated to the class have greater weights, which makes the more discriminating variables contribute more to the model. At the same time, FWMNBM does not have to calculate the conditional probability between variables, thus it is less restricted by the number of training data samples. Compared with MHNBM, FWMNBM has better performance, and its effectiveness is validated through the numerical cases of a simulation example and a practical case of Zhoushan thermal power plant (ZTPP), China.
翻译:随着情报和一体化的不断增强,大规模工业流程中往往存在大量两种价值的变数(通常以0或1值的形式储存),这些变数无法通过传统的监测方法,如LDA、CPA和PLS等,有效地处理这些变数。最近,首次开发了一种混合的、隐蔽的天真的Bayesian模型(MHNBM),以利用两种价值和连续的变数来监测异常情况。虽然MHNBM是有效的,但仍有一些需要改进的缺点。对于MHNBM而言,与其他变数关系较大的变数的变数比重更大,无法保证更大的权重被分配到比较有区别的变数。此外,有条件的概率必须根据历史数据计算。当培训数据少时,连续变数之间的有条件的概率往往一致分布,从而影响MHMBMMMMBM的性能。在这里开发了一个加权的变数,克服上述缺点。FWMNBMBMBM的变数比比重更大一些。