A complete and continuous map of the Lattice Isometry Space for all 3-dimensional lattices

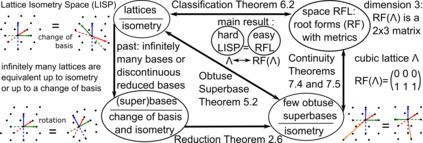
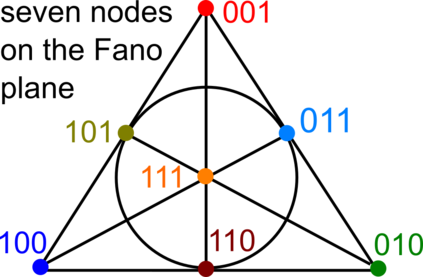
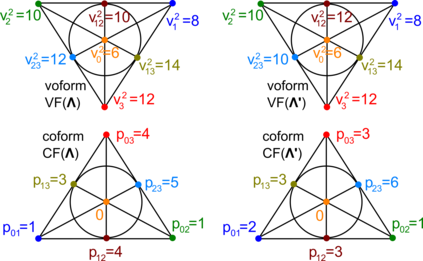
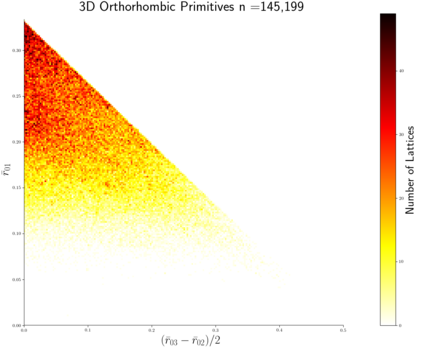
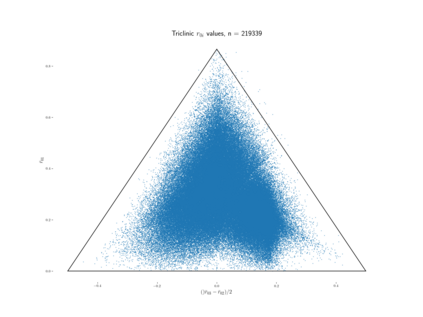
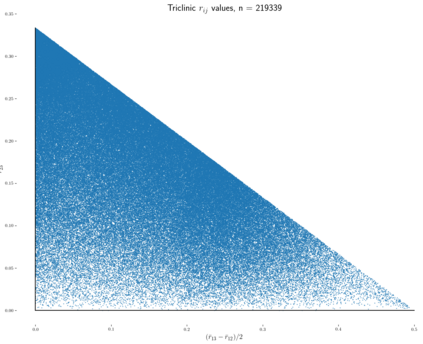
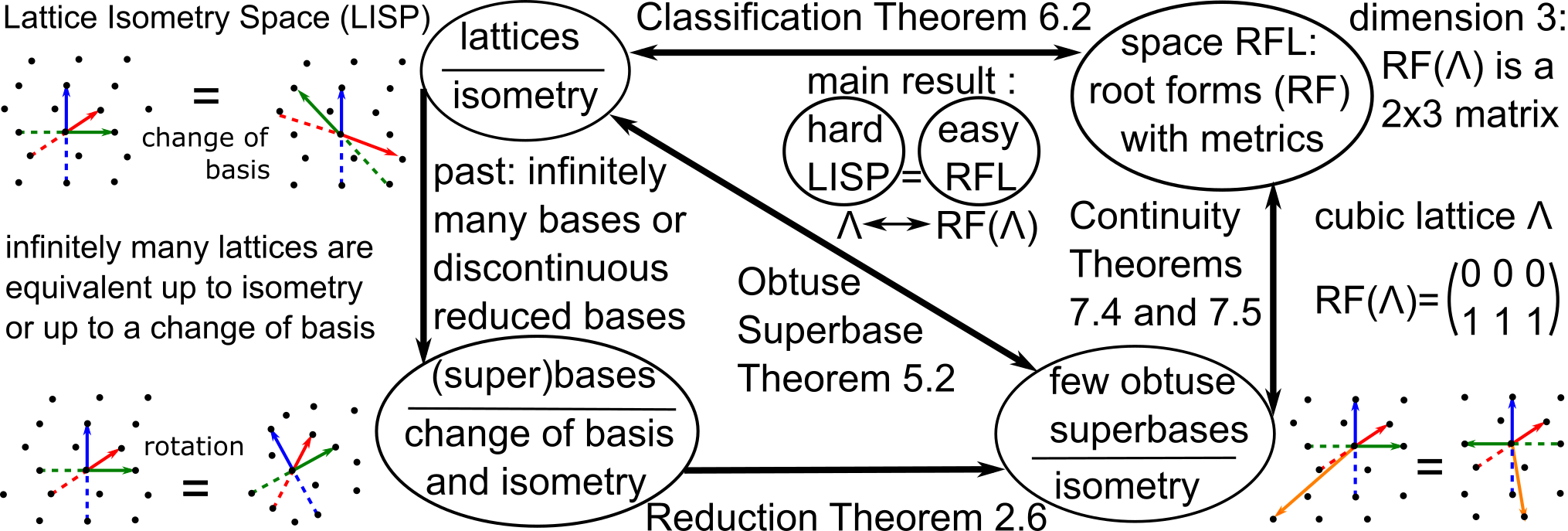
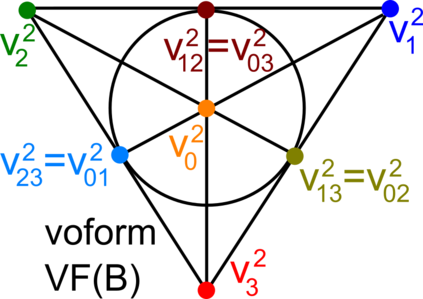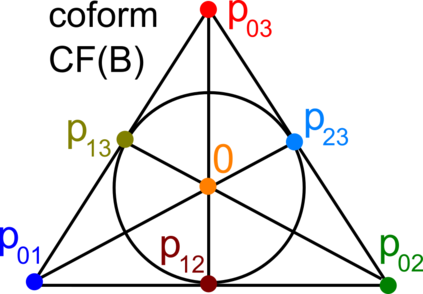This paper extends the recently obtained complete and continuous map of the Lattice Isometry Space (LISP) to the practical case of dimension 3. A periodic 3-dimensional lattice is an infinite set of all integer linear combinations of basis vectors in Euclidean 3-space. Motivated by crystal structures determined in a rigid form, we study lattices up to rigid motion or isometry, which is a composition of translations, rotations and reflections. The resulting space LISP consists of infinitely many isometry classes of lattices. In dimension 3, we parameterise this continuous space LISP by six coordinates and introduce new metrics satisfying the metric axioms and continuity under all perturbations. This parameterisation helps to visualise hundreds of thousands of real crystal lattices from the Cambridge Structural Database for the first time.