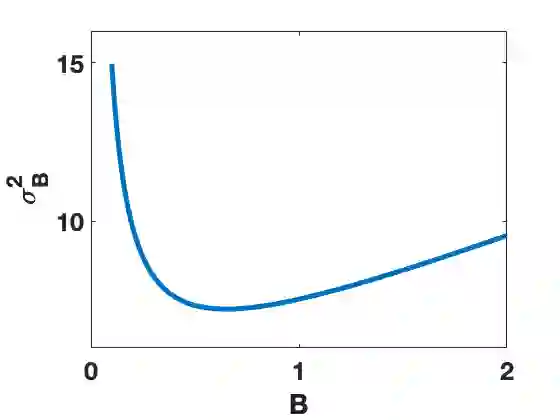
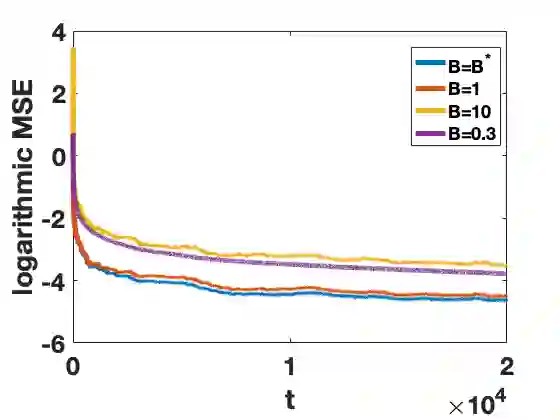
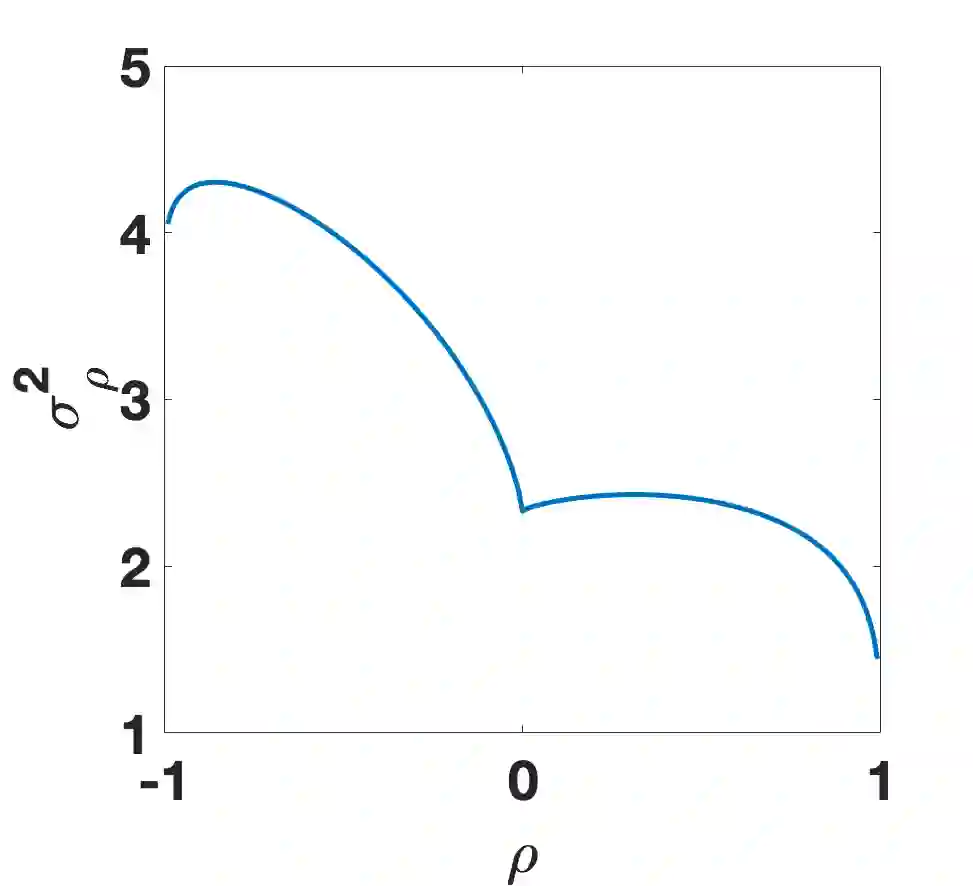
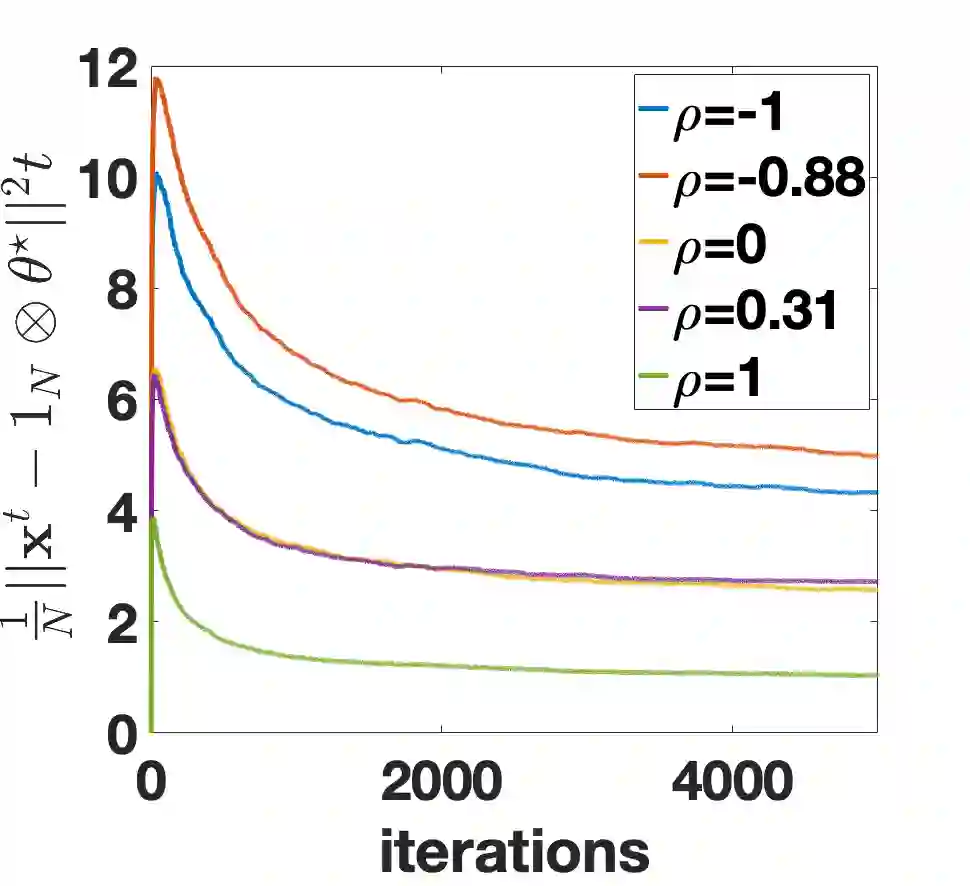
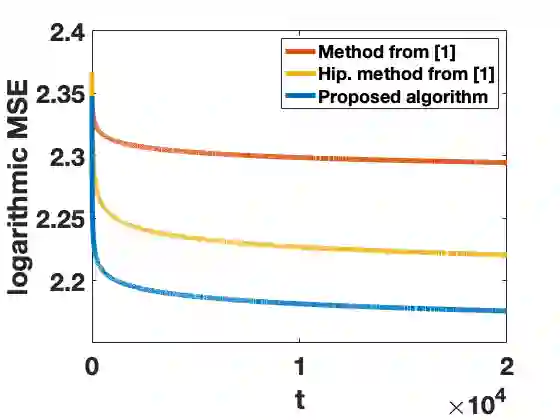
We consider distributed recursive estimation of consensus+innovations type in the presence of heavy-tailed sensing and communication noises. We allow that the sensing and communication noises are mutually correlated while independent identically distributed (i.i.d.) in time, and that they may both have infinite moments of order higher than one (hence having infinite variances). Such heavy-tailed, infinite-variance noises are highly relevant in practice and are shown to occur, e.g., in dense internet of things (IoT) deployments. We develop a consensus+innovations distributed estimator that employs a general nonlinearity in both consensus and innovations steps to combat the noise. We establish the estimator's almost sure convergence, asymptotic normality, and mean squared error (MSE) convergence. Moreover, we establish and explicitly quantify for the estimator a sublinear MSE convergence rate. We then quantify through analytical examples the effects of the nonlinearity choices and the noises correlation on the system performance. Finally, numerical examples corroborate our findings and verify that the proposed method works in the simultaneous heavy-tail communication-sensing noise setting, while existing methods fail under the same noise conditions.
翻译:我们认为,在超速的感知和通信噪音的情况下,对协商一致和革新类型进行分布式的重复估计是重复性的。我们允许感知和通讯噪音在时间上相互关联,同时独立地进行相同的分配(即d.d.),而且它们都有无限的秩序时刻高于一个时刻(因此差异很大 ) 。这种重尾、无限变化的噪音在实践中具有高度相关性,并显示会发生,例如,在密集的事物互联网(IoT)的部署中。我们开发了一个共识加创新分布式估计符,在共识和创新步骤中采用一般的非线性来对付噪音。我们建立了估计器几乎肯定的趋同性、无症状的正常性和平均的平方差(MSE)趋同。此外,我们为估计器建立并明确量化一个子线性MSE趋同率。我们随后通过分析实例来量化非线性选择的影响和噪音对系统性能的关联性。最后,数字例子证实了我们的调查结果,并核实了我们提出的方法在同时设定重度的噪声测量条件下如何工作。