Learning task-specific features for 3D pointcloud graph creation

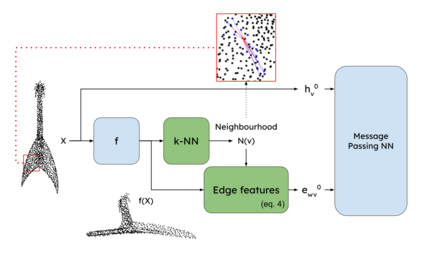
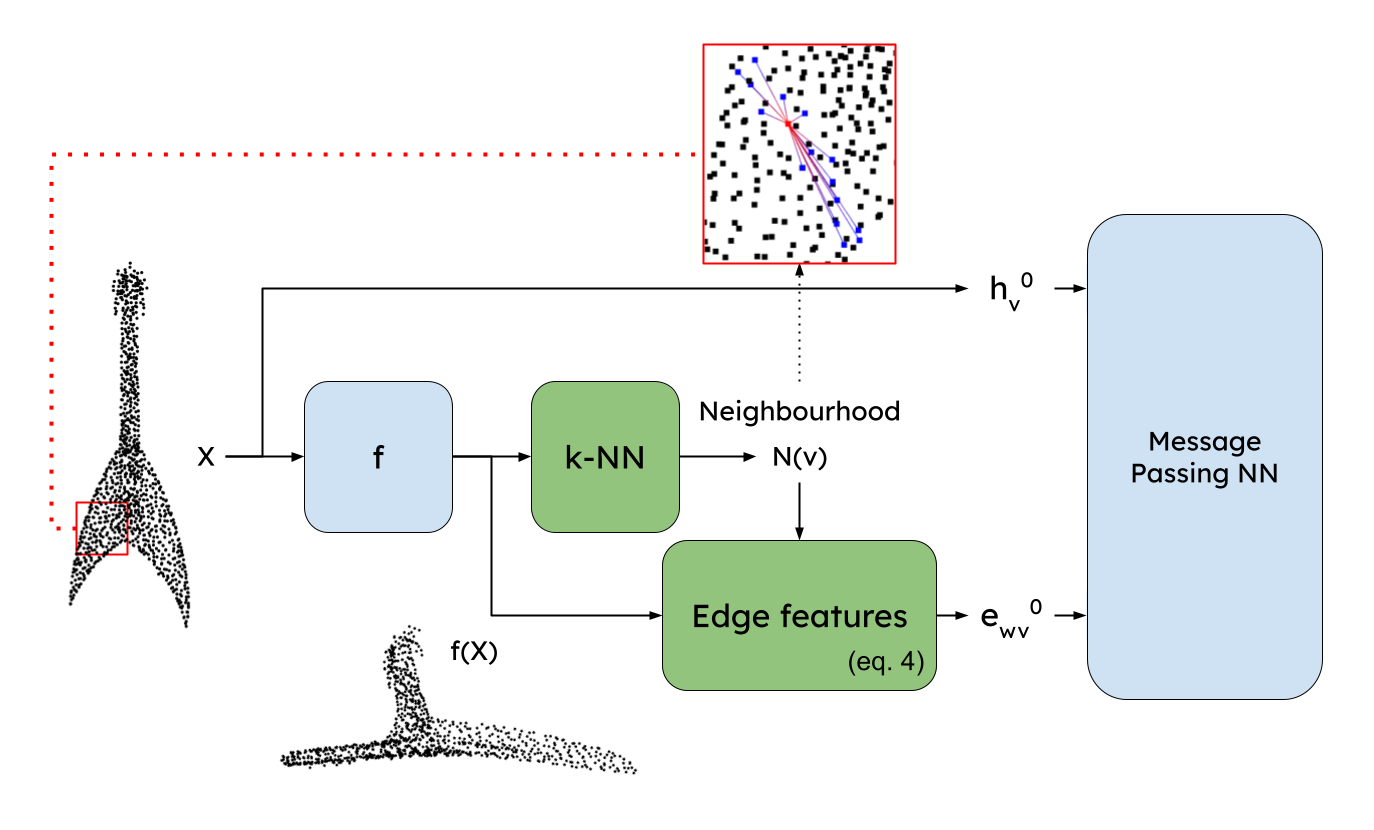
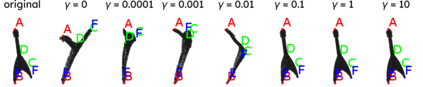Processing 3D pointclouds with Deep Learning methods is not an easy task. A common choice is to do so with Graph Neural Networks, but this framework involves the creation of edges between points, which are explicitly not related between them. Historically, naive and handcrafted methods like k Nearest Neighbors (k-NN) or query ball point over xyz features have been proposed, focusing more attention on improving the network than improving the graph. In this work, we propose a more principled way of creating a graph from a 3D pointcloud. Our method is based on performing k-NN over a transformation of the input 3D pointcloud. This transformation is done by an Multi-Later Perceptron (MLP) with learnable parameters that is optimized through backpropagation jointly with the rest of the network. We also introduce a regularization method based on stress minimization, which allows to control how distant is the learnt graph from our baseline: k-NN over xyz space. This framework is tested on ModelNet40, where graphs generated by our network outperformed the baseline by 0.3 points in overall accuracy.