A new approach to proper orthogonal decomposition with difference quotients

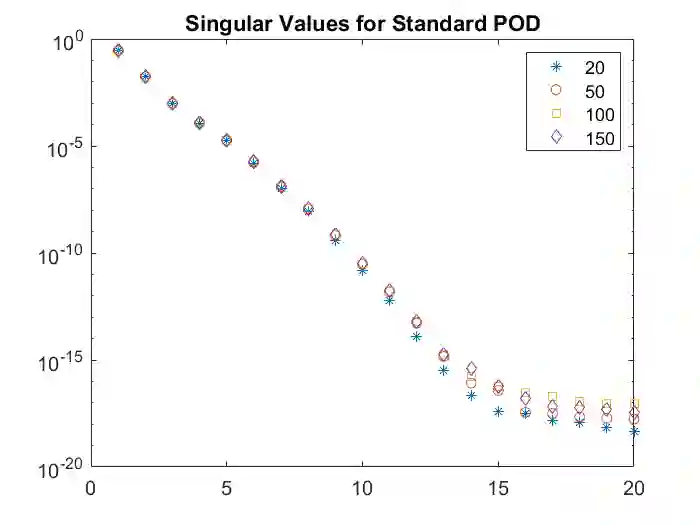
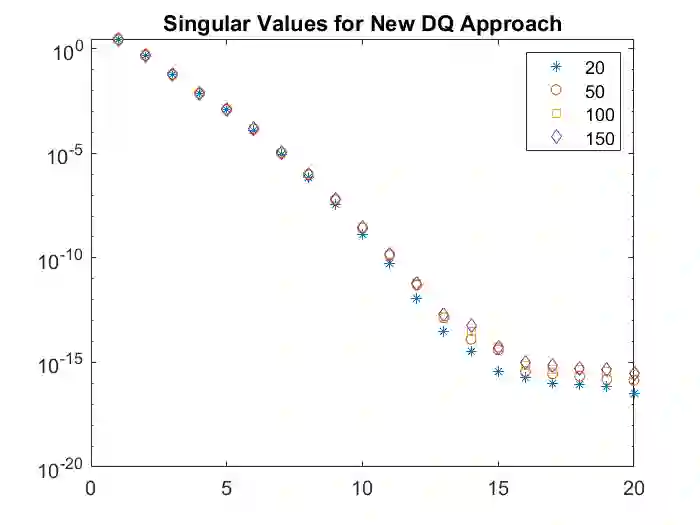
In a recent work [B. Koc et al., arXiv:2010.03750, SIAM J. Numer. Anal., to appear], the authors showed that including difference quotients (DQs) is necessary in order to prove optimal pointwise in time error bounds for proper orthogonal decomposition (POD) reduced order models of the heat equation. In this work, we introduce a new approach to including DQs in the POD procedure. Instead of computing the POD modes using all of the snapshot data and DQs, we only use the first snapshot along with all of the DQs and special POD weights. We show that this approach retains all of the numerical analysis benefits of the standard POD DQ approach, while using a POD data set that has half the number of snapshots as the standard POD DQ approach, i.e., the new approach is more computationally efficient. We illustrate our theoretical results with numerical experiments.