Robust Eigenvectors of Symmetric Tensors

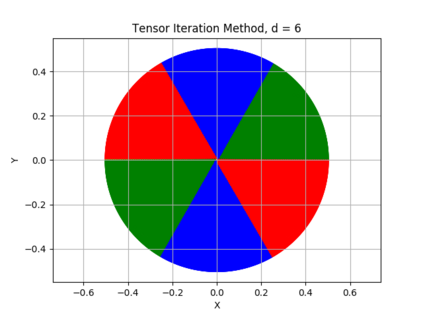
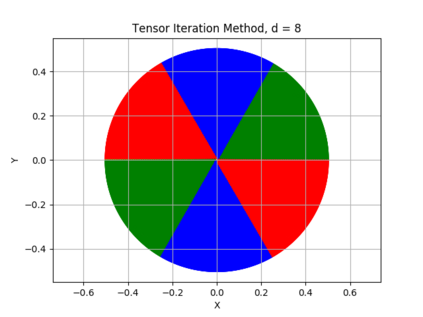
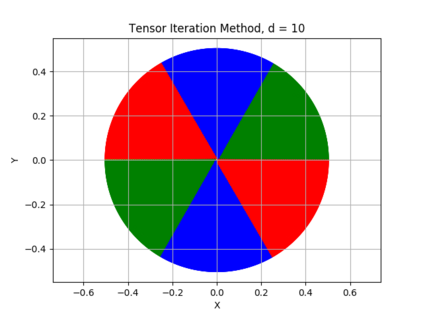
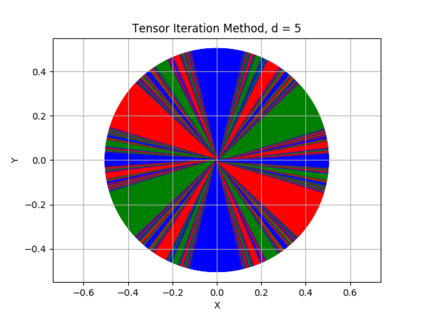
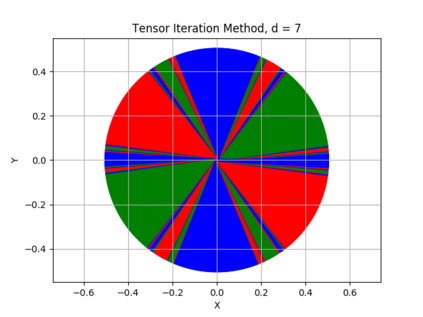
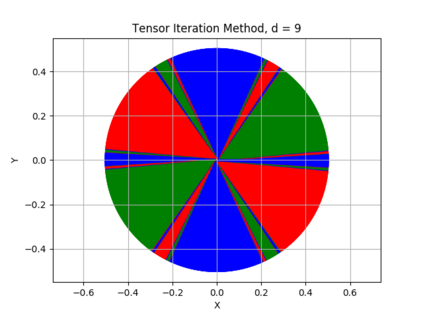
The {\em tensor power method} generalizes the matrix power method to higher order arrays, or tensors. Like in the matrix case, the fixed points of the tensor power method are the eigenvectors of the tensor. While every real symmetric matrix has an eigendecomposition, the vectors generating a symmetric decomposition of a real symmetric tensor are not always eigenvectors of the tensor. In this paper we show that whenever an eigenvector {\em is} a generator of the symmetric decomposition of a symmetric tensor, then (if the order of the tensor is sufficiently high) this eigenvector is {\em robust} , i.e., it is an attracting fixed point of the tensor power method. We exhibit new classes of symmetric tensors whose symmetric decomposition consists of eigenvectors. Generalizing orthogonally decomposable tensors, we consider {\em equiangular tight frame decomposable} and {\em equiangular set decomposable} tensors. Our main result implies that such tensors can be decomposed using the tensor power method.