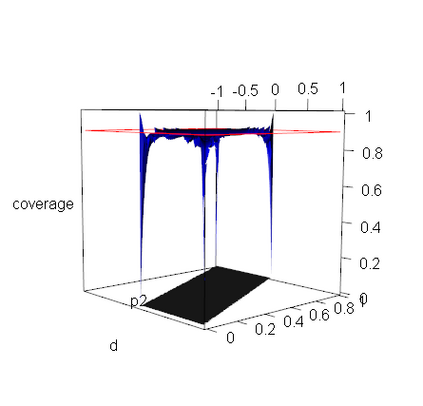
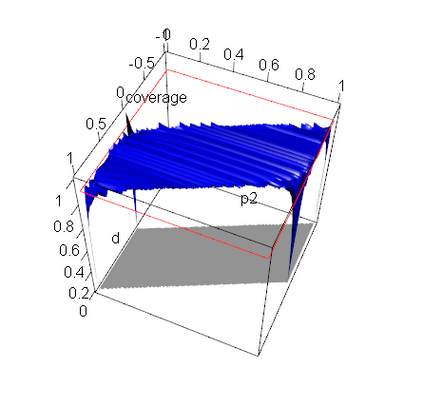
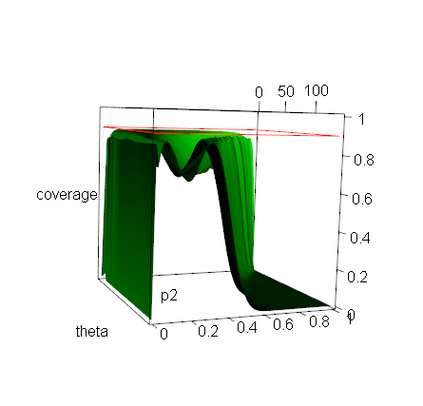
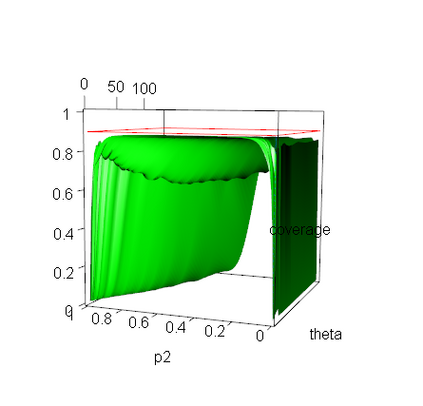
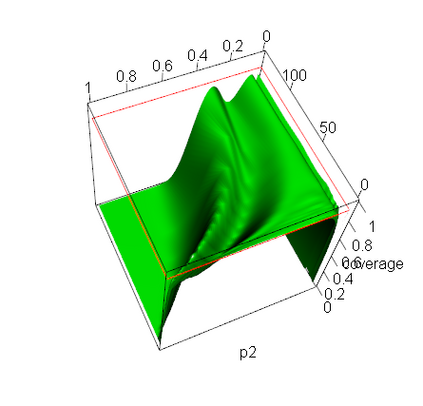
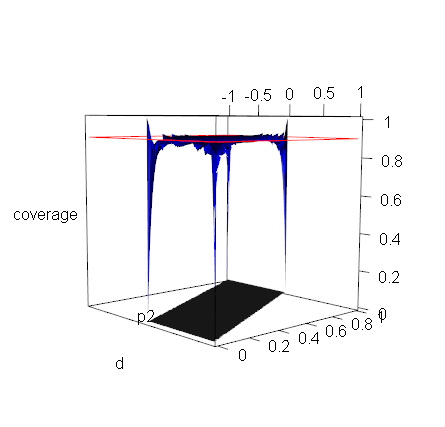
A reasonable confidence interval should have a confidence coefficient no less than the given nominal level and a small expected length to reliably and accurately estimate the parameter of interest, and the bootstrap interval is considered to be an efficient interval estimation technique. In this paper, we offer a first attempt at computing the coverage probability and expected length of a parametric or percentile bootstrap interval by exact probabilistic calculation for any fixed sample size. This method is applied to the basic bootstrap intervals for functions of binomial proportions and a normal mean. None of these intervals, however, are found to have a correct confidence coefficient, which leads to illogical conclusions including that the bootstrap interval is narrower than the z-interval when estimating a normal mean. This raises a general question of how to utilize bootstrap intervals appropriately in practice since the sample size is typically fixed.
翻译:暂无翻译