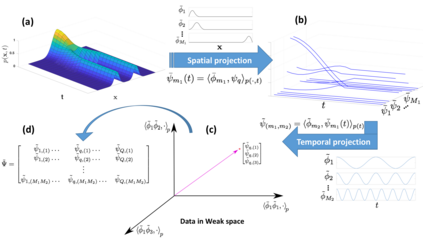
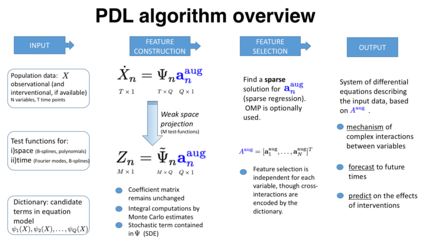
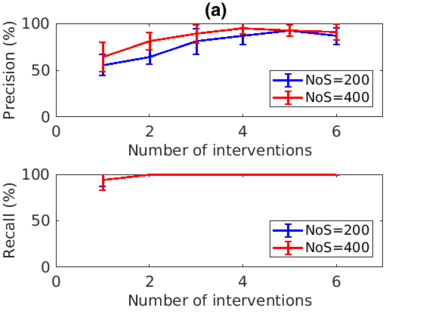
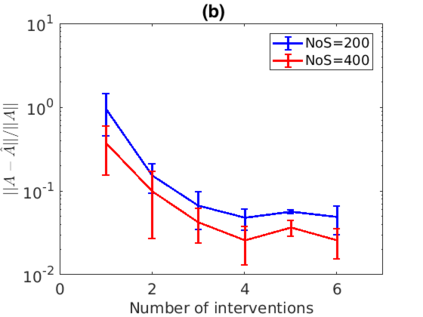
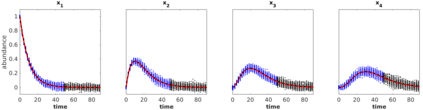
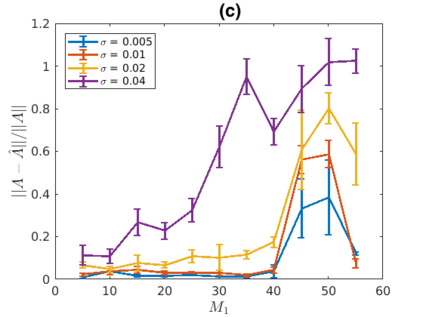
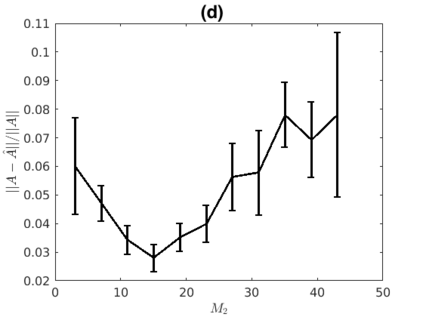
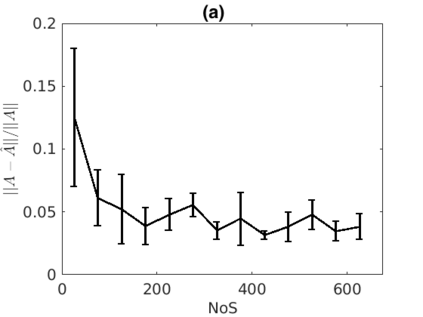
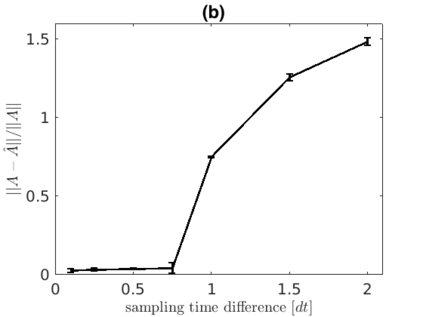
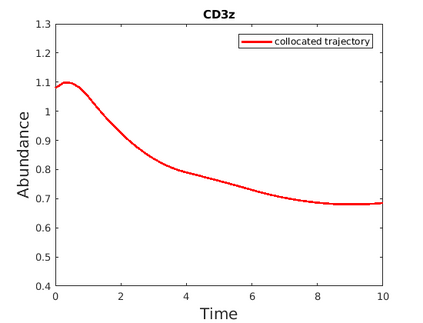
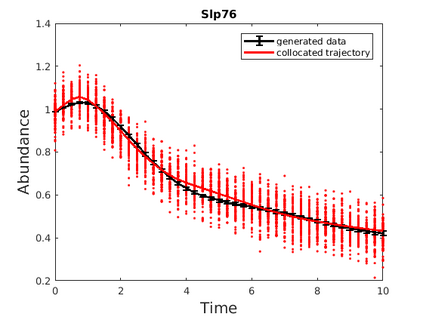
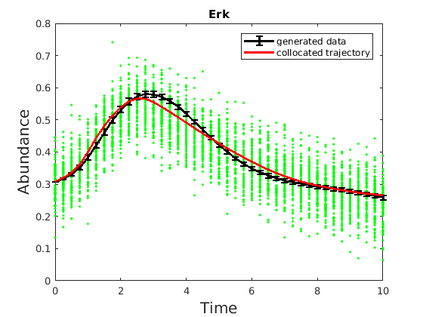
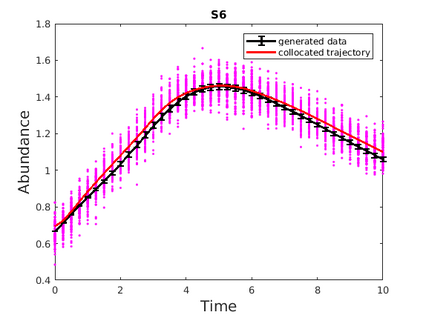
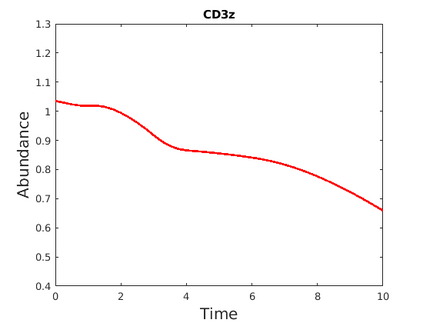
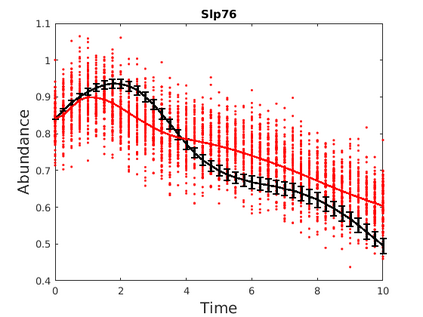
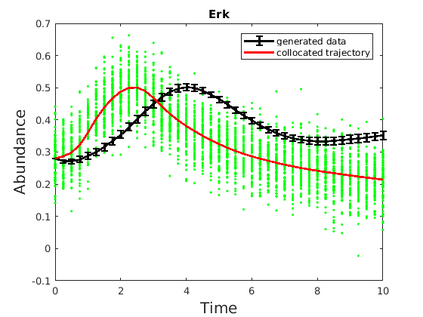
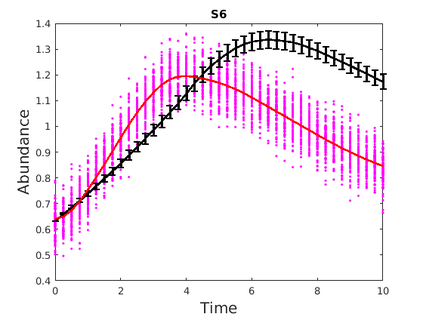
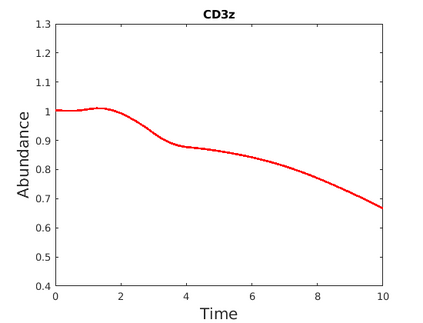
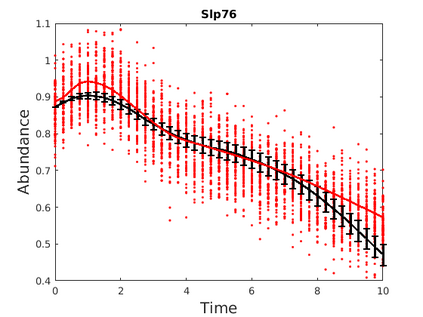
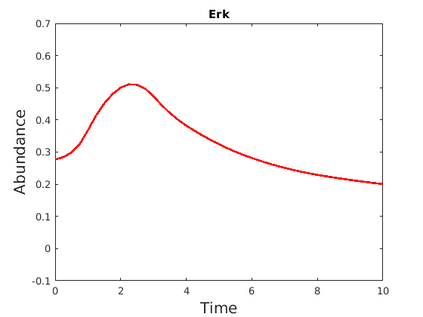
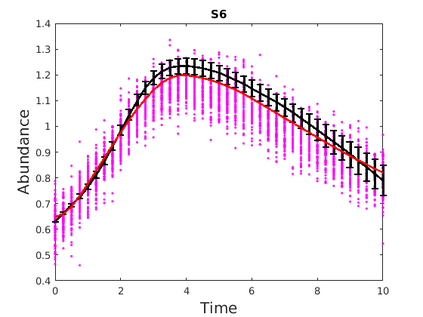
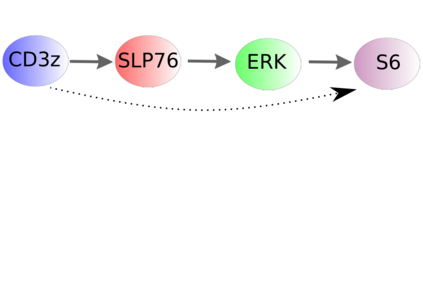
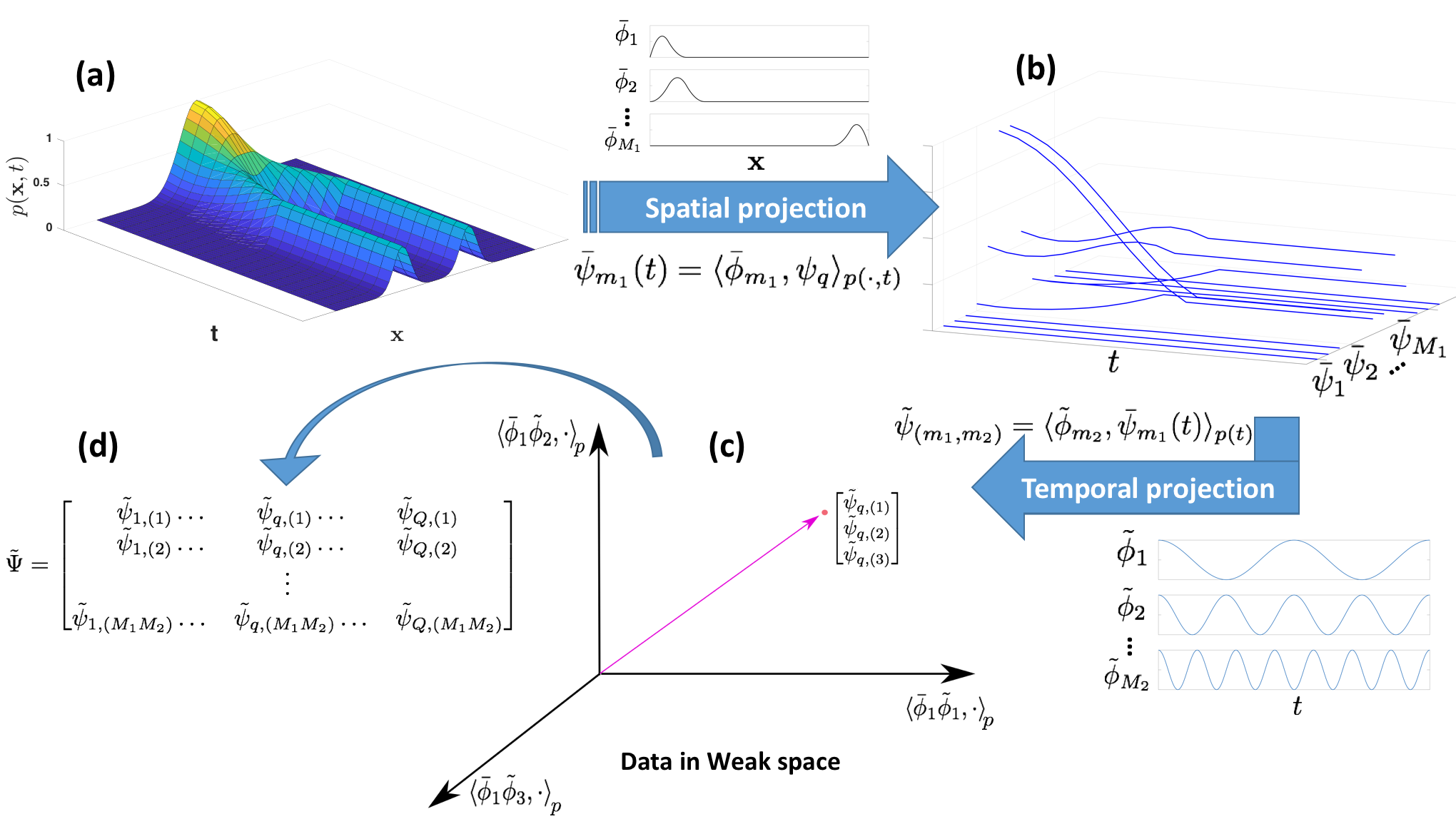
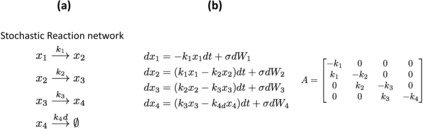Inferring the driving equations of a dynamical system from population or time-course data is important in several scientific fields such as biochemistry, epidemiology, financial mathematics and many others. Despite the existence of algorithms that learn the dynamics from trajectorial measurements there are few attempts to infer the dynamical system straight from population data. In this work, we deduce and then computationally estimate the Fokker-Planck equation which describes the evolution of the population's probability density, based on stochastic differential equations. Then, following the USDL approach, we project the Fokker-Planck equation to a proper set of test functions, transforming it into a linear system of equations. Finally, we apply sparse inference methods to solve the latter system and thus induce the driving forces of the dynamical system. Our approach is illustrated in both synthetic and real data including non-linear, multimodal stochastic differential equations, biochemical reaction networks as well as mass cytometry biological measurements.
翻译:从人口或时间过程数据推断动态系统的驱动方程式,在生物化学、流行病学、金融数学和其他许多科学领域都很重要。尽管存在着从轨迹测量中学习动态的算法,但很少尝试从人口数据中直接推断动态系统。在这项工作中,我们根据随机差异方程式,推论并随后计算估算了Fokker-Planck方程式,该方程式描述了人口概率密度的变化。随后,根据USDL方法,我们预测Fokker-Planck方程式为一套适当的测试功能,将其转化为直线方程式系统。最后,我们采用稀有的推论方法解决后一种系统,从而引导动态系统的驱动力。我们的方法在合成和真实数据中都有说明,包括非线性、多式随机差异方程式、生物化学反应网络以及大规模细胞测量生物测量。