On Krylov Methods for Large Scale CBCT Reconstruction

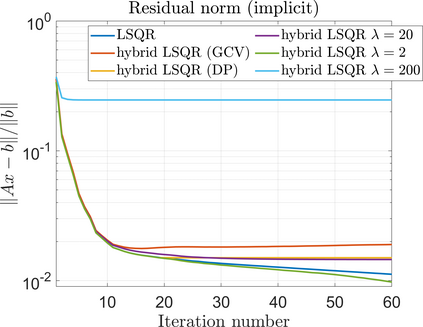
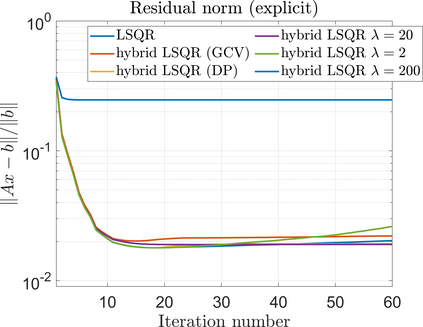
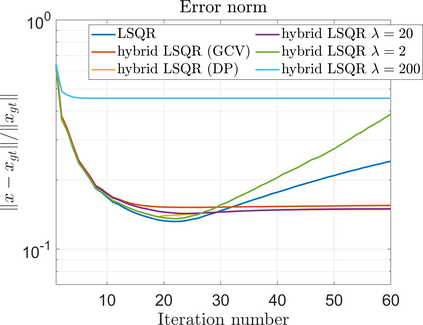
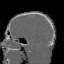
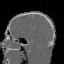
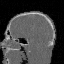
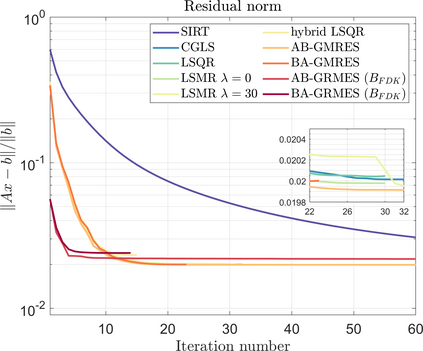
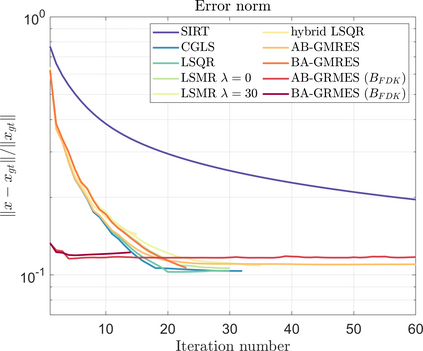
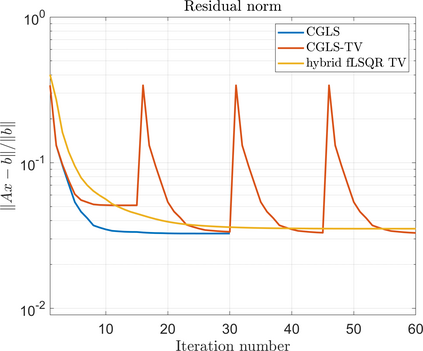
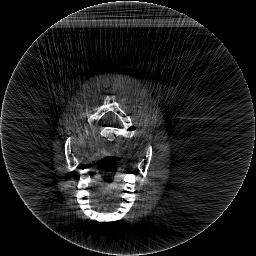
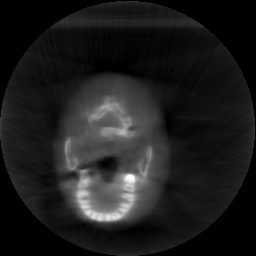
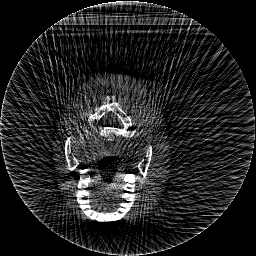
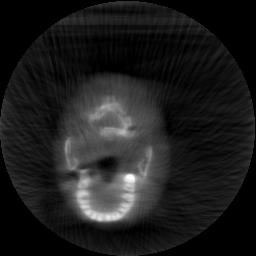
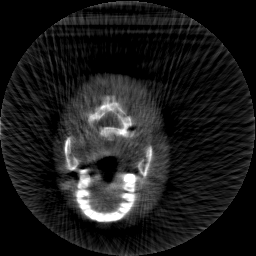
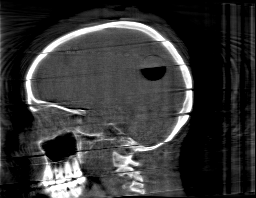
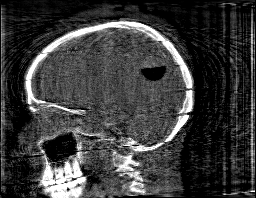
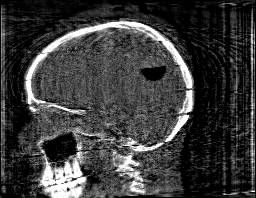
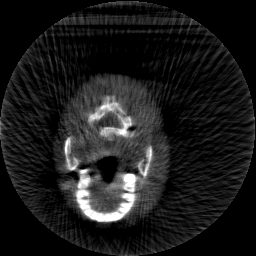
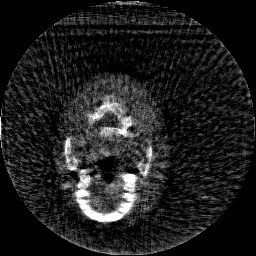
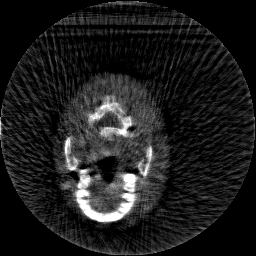
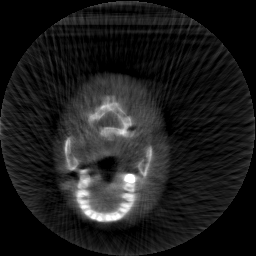
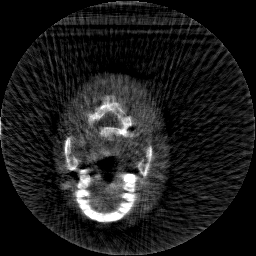
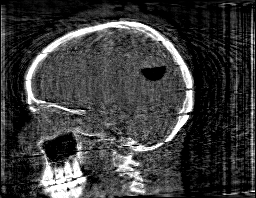
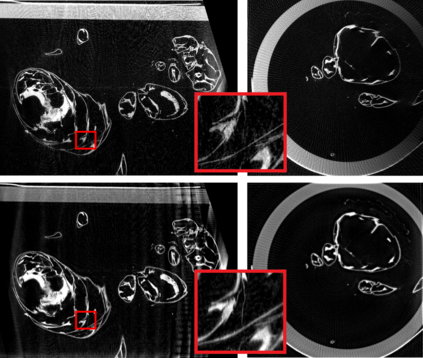
Krylov subspace methods are a powerful family of iterative solvers for linear systems of equations, which are commonly used for inverse problems due to their intrinsic regularization properties. Moreover, these methods are naturally suited to solve large-scale problems, as they only require matrix-vector products with the system matrix (and its adjoint) to compute approximate solutions, and they display a very fast convergence. Even if this class of methods has been widely researched and studied in the numerical linear algebra community, its use in applied medical physics and applied engineering is still very limited. e.g. in realistic large-scale Computed Tomography (CT) problems, and more specifically in Cone Beam CT (CBCT). This work attempts to breach this gap by providing a general framework for the most relevant Krylov subspace methods applied to 3D CT problems, including the most well-known Krylov solvers for non-square systems (CGLS, LSQR, LSMR), possibly in combination with Tikhonov regularization, and methods that incorporate total variation (TV) regularization. This is provided within an open source framework: the Tomographic Iterative GPU-based Reconstruction (TIGRE) toolbox, with the idea of promoting accessibility and reproducibility of the results for the algorithms presented. Finally, numerical results in synthetic and real-world 3D CT applications (medical CBCT and {\mu}-CT datasets) are provided to showcase and compare the different Krylov subspace methods presented in the paper, as well as their suitability for different kinds of problems.