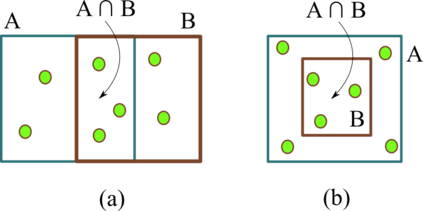
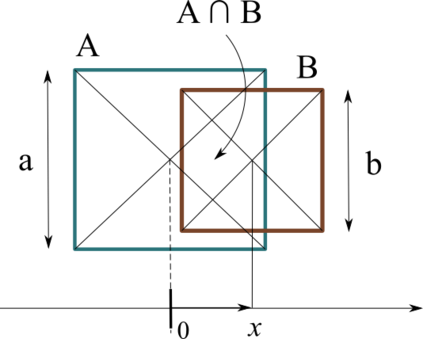
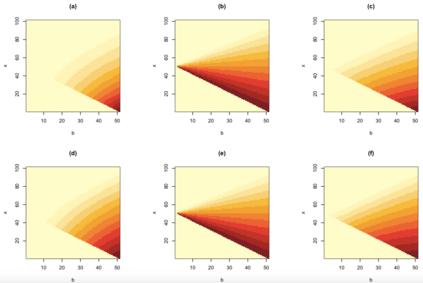
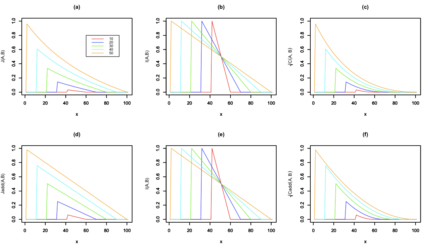
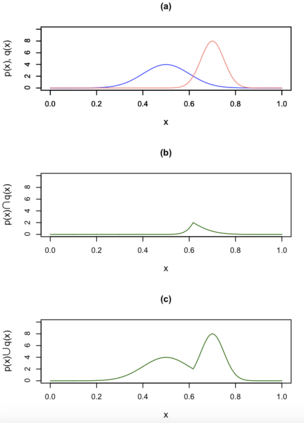
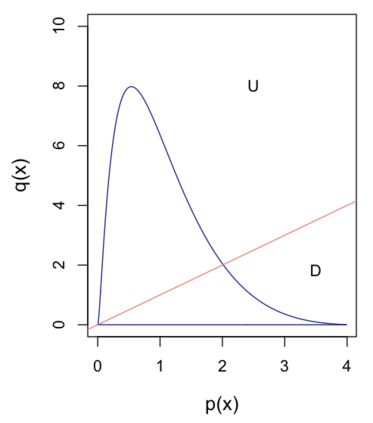
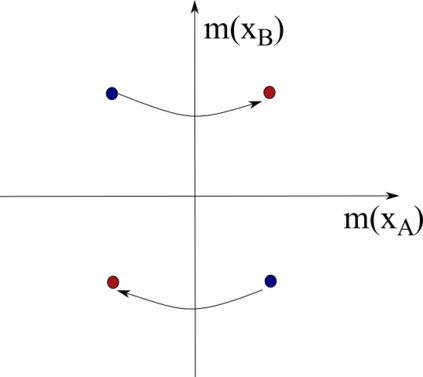
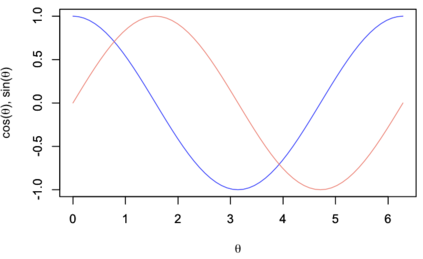
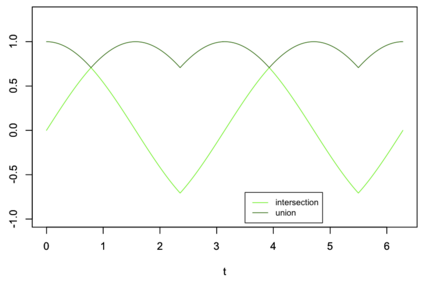
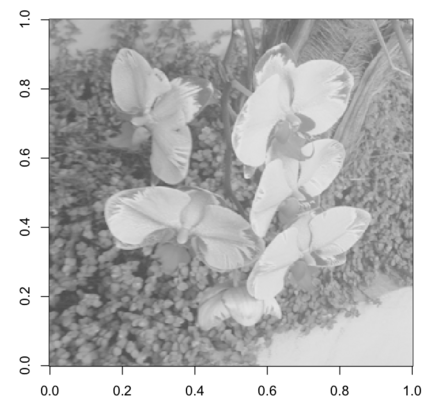
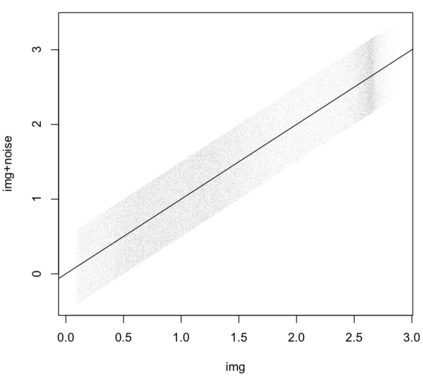
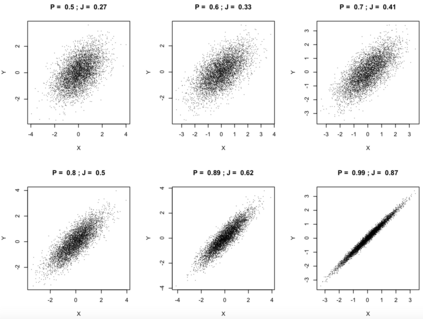
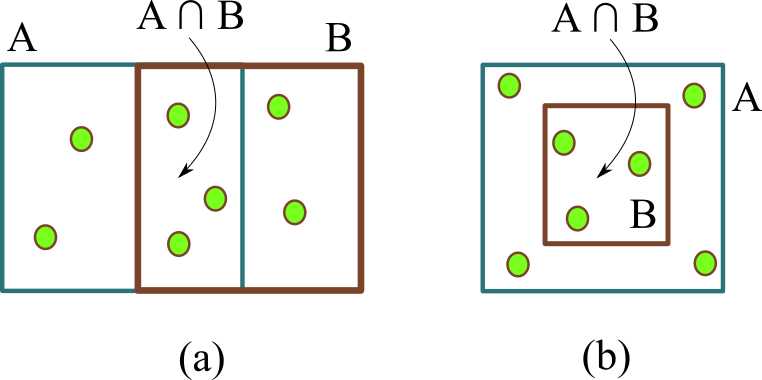
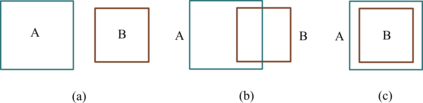Quantifying the similarity between two mathematical structures or datasets constitutes a particularly interesting and useful operation in several theoretical and applied problems. Aimed at this specific objective, the Jaccard index has been extensively used in the most diverse types of problems, also motivating some respective generalizations. The present work addresses further generalizations of this index, including its modification into a coincidence index capable of accounting also for the level of relative interiority between the two compared entities, as well as respective extensions for sets in continuous vector spaces, the generalization to multiset addition, densities and generic scalar fields, as well as a means to quantify the joint interdependence between two random variables. The also interesting possibility to take into account more than two sets has also been addressed, including the description of an index capable of quantifying the level of chaining between three structures. Several of the described and suggested eneralizations have been illustrated with respect to numeric case examples. It is also posited that these indices can play an important role while analyzing and integrating datasets in modeling approaches and pattern recognition activities, including as a measurement of clusters similarity or separation and as a resource for representing and analyzing complex networks.
翻译:计算两个数学结构或数据集之间的相似性,是几个理论和应用问题中特别有趣和有用的操作。为了这一具体目标,在最多样化的各类问题中广泛使用“雅克卡”指数,也促使某些不同的概括性。目前的工作涉及该指数的进一步概括性,包括将其修改为可同时计算两个比较实体之间相对内分化程度的巧合性指数,以及连续矢量空间各组的扩展、多集添加的概括性、密度和通用标度字段,以及量化两个随机变量之间的联合相互依存性的一种手段。还探讨了考虑两个以上数据集的令人感兴趣的可能性,包括说明能够量化三个结构之间链化程度的指数。所描述和建议的累进性指数中有一些已经用数字案例的例子加以说明。还假定,这些指数在分析和整合数据集的同时,在模拟方法和模式识别活动中可以发挥重要作用,包括作为群集的测量或分离,以及作为代表和复杂分析网络的资源。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem