Parameters estimation in a 3-parameters p-star model

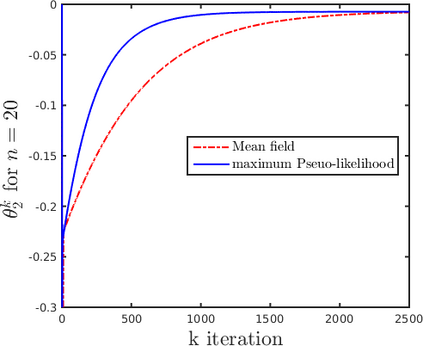
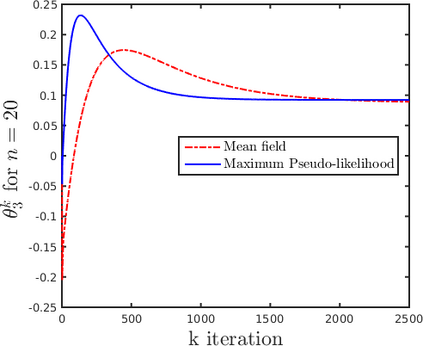
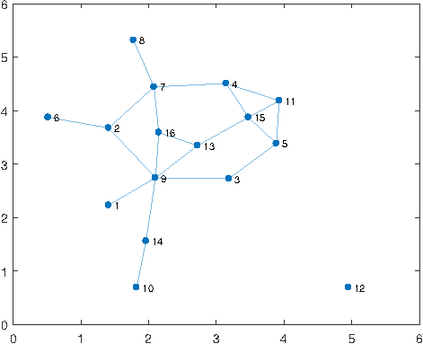
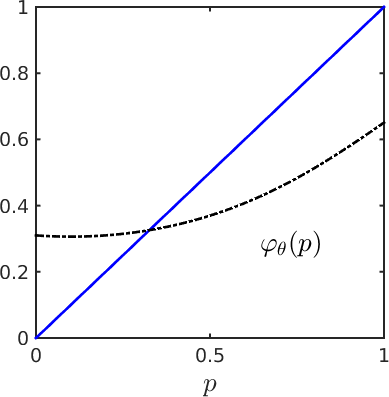
An important issue in social network analysis refers to the development of algorithms for estimating optimal parameters of a social network model, using data available from the network itself. This entails solving an optimization problem. In the paper, we propose a new method for parameters estimation in a specific social network model, namely, the so-called p-star model with three parameters. The method is based on the mean-field approximation of the moments associated with the three subgraphs defining the model, namely: the mean numbers of edges, two-stars, and triangles. A modified gradient ascent method is applied to maximize the log-likelihood function of the p-star model, in which the components of the gradient are computed using approximate values of the moments. Compared to other existing iterative methods for parameters estimation, which are computationally very expensive when the number of vertices becomes large, such as gradient ascent applied to maximum log-pseudo- likelihood estimation, the proposed approach has the advantage of a much cheaper cost per iteration, which is practically independent of the number of vertices.