Complete and bi-continuous invariant of protein backbones under rigid motion

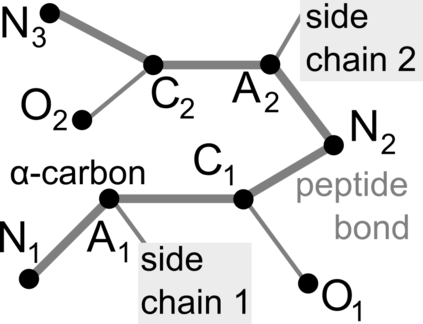
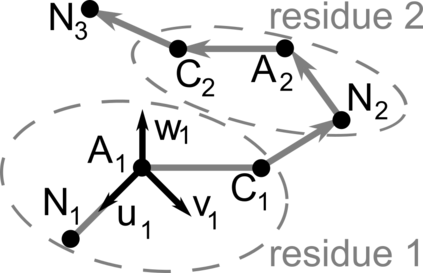
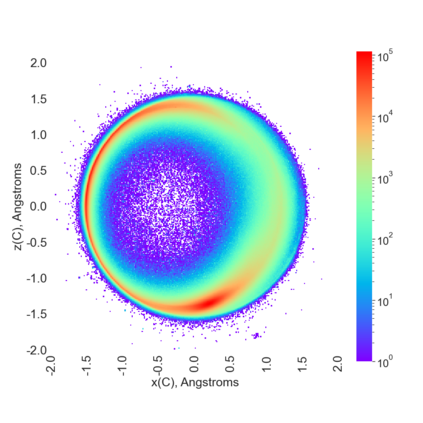
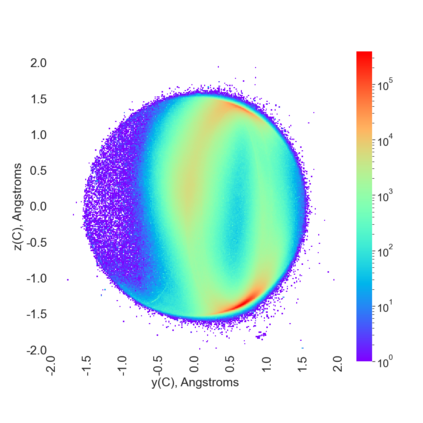
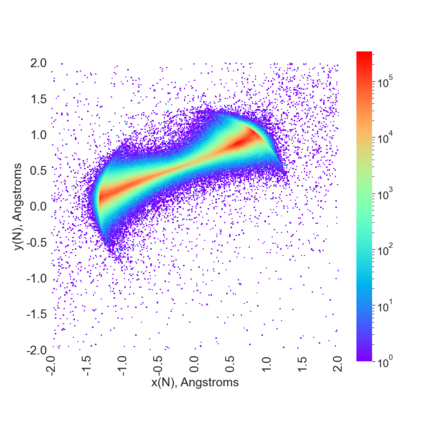
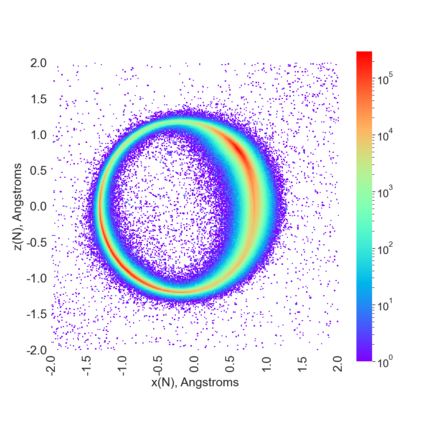
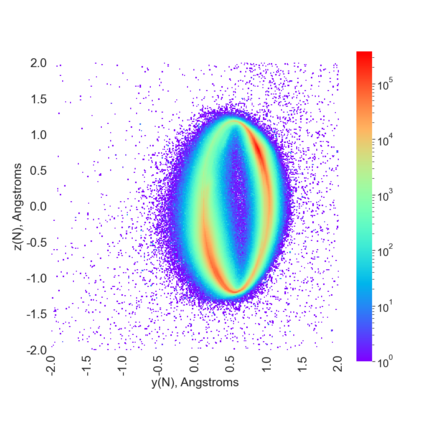
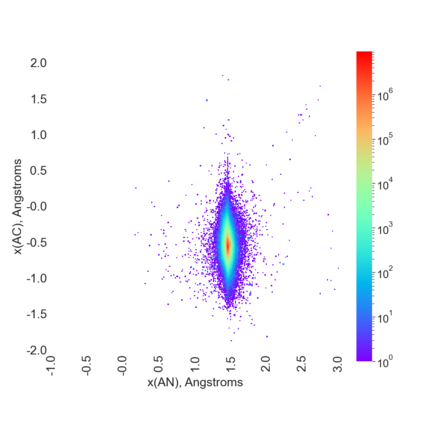
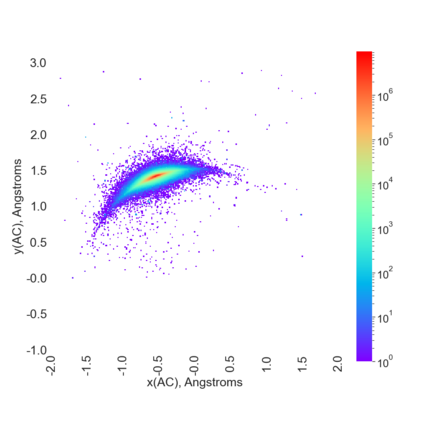
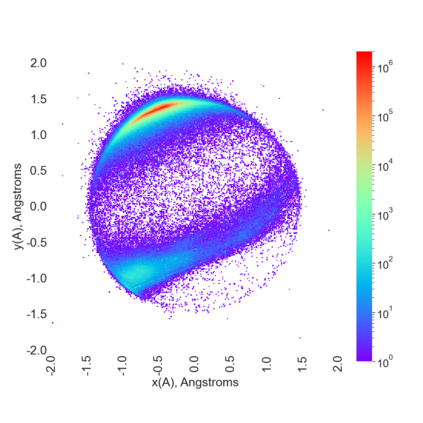
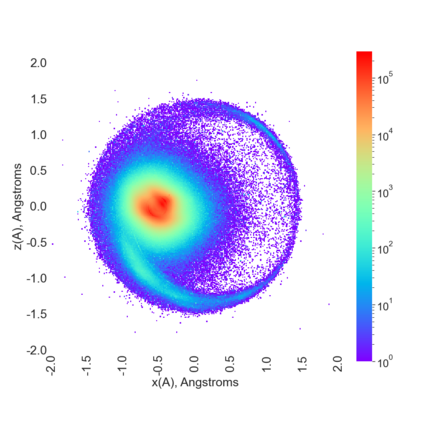
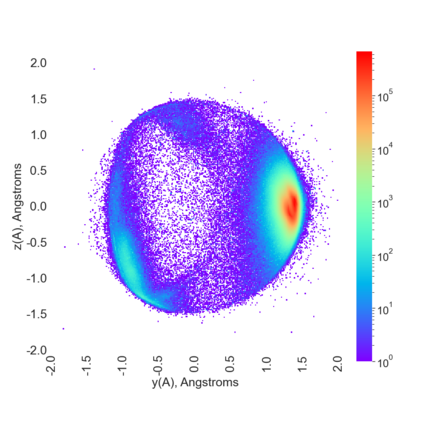
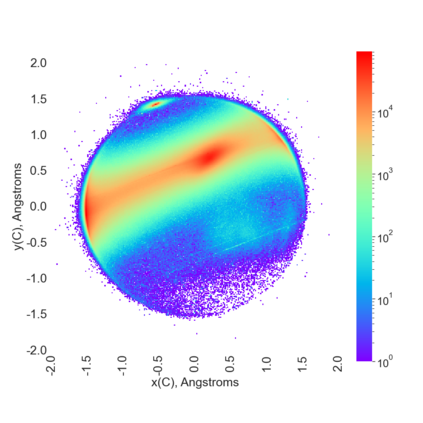
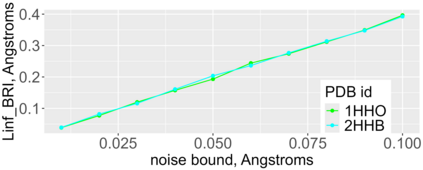
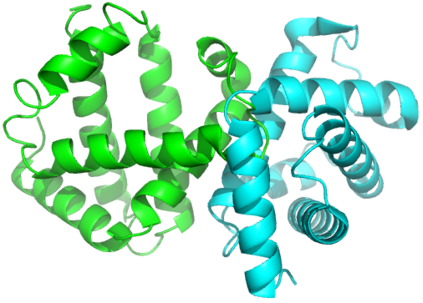
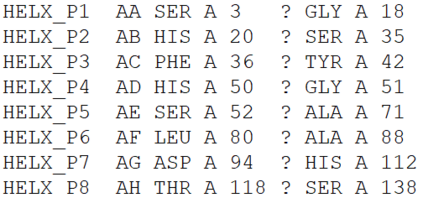
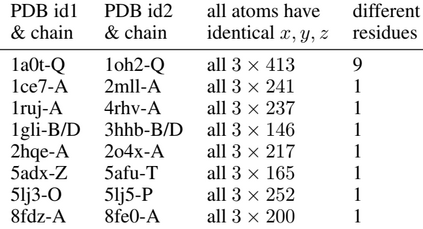
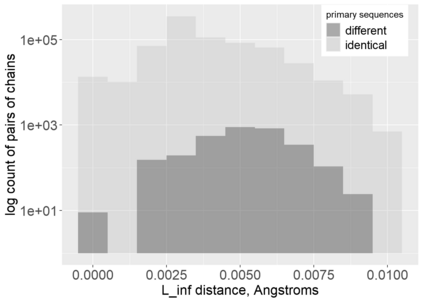
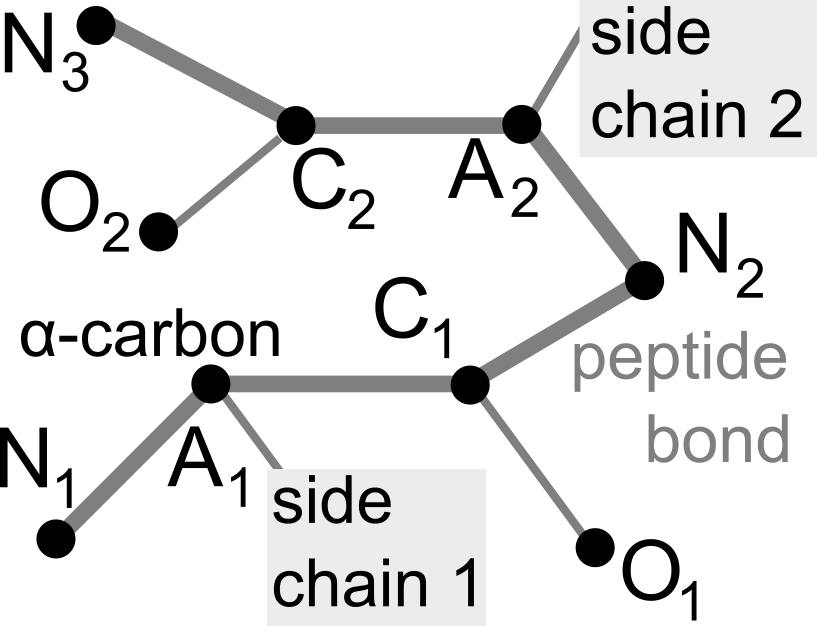
Proteins are large biomolecules that regulate all living organisms and consist of one or several chains.The primary structure of a protein chain is a sequence of amino acid residues whose three main atoms (alpha-carbon, nitrogen, and carboxyl carbon) form a protein backbone. The tertiary (geometric) structure is the rigid shape of a protein chain represented by atomic positions in a 3-dimensional space. Because different geometric structures often have distinct functional properties, it is important to continuously quantify differences in rigid shapes of protein backbones. Unfortunately, many widely used similarities of proteins fail axioms of a distance metric and discontinuously change under tiny perturbations of atoms. This paper develops a complete invariant under rigid motion, which defines a Lipschitz bi-continuous bijection from all rigid classes of protein backbones to a well-defined invariant space. The new invariant detected thousands of (near-)duplicates in the Protein Data Bank, whose presence inevitably skews machine learning predictions. The resulting invariant space allows low-dimensional maps with analytically defined coordinates that reveal substantial variability in the protein universe.