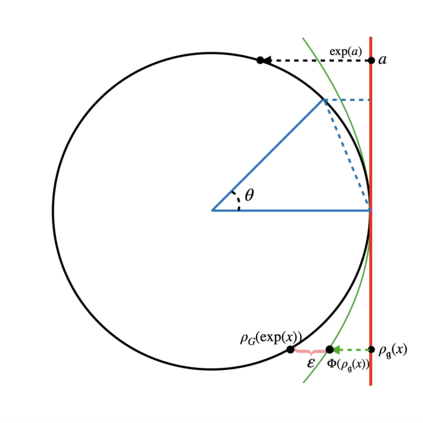
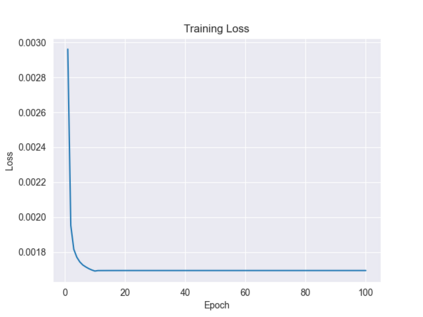
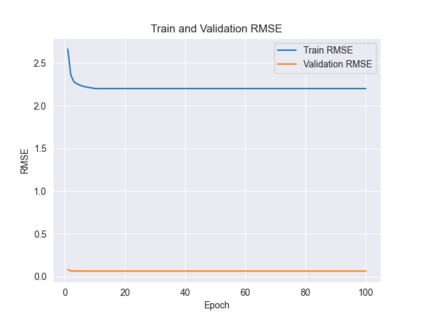
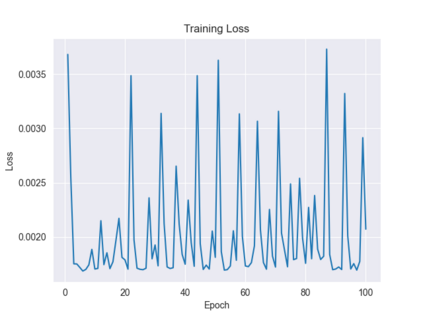
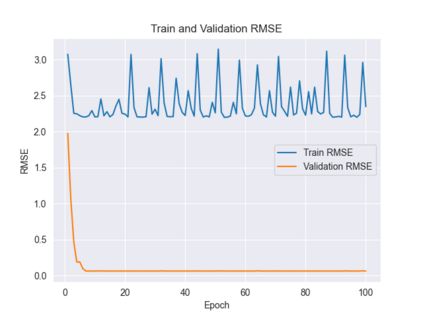
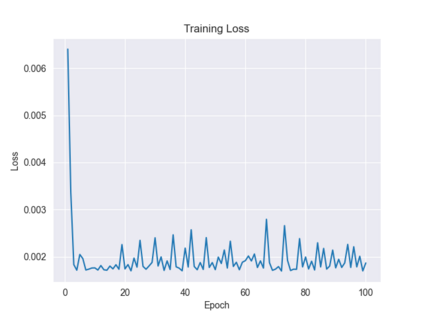
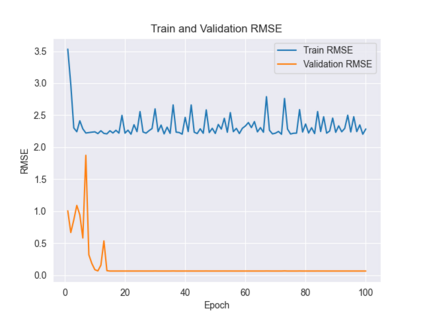
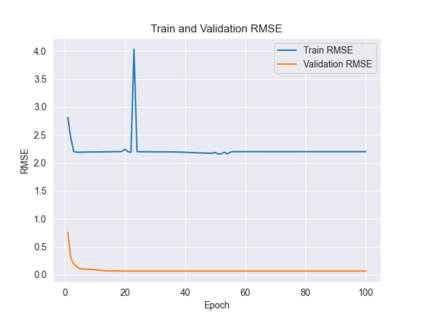
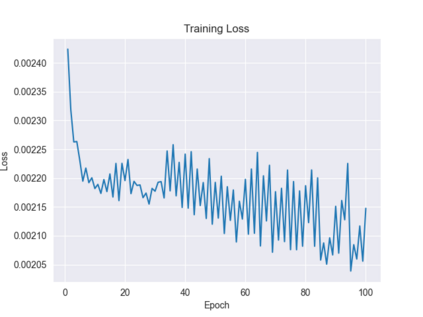
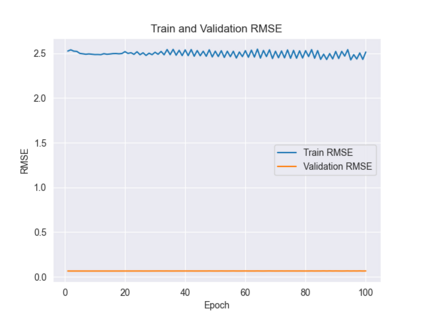
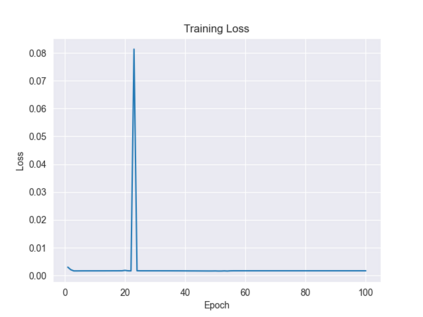
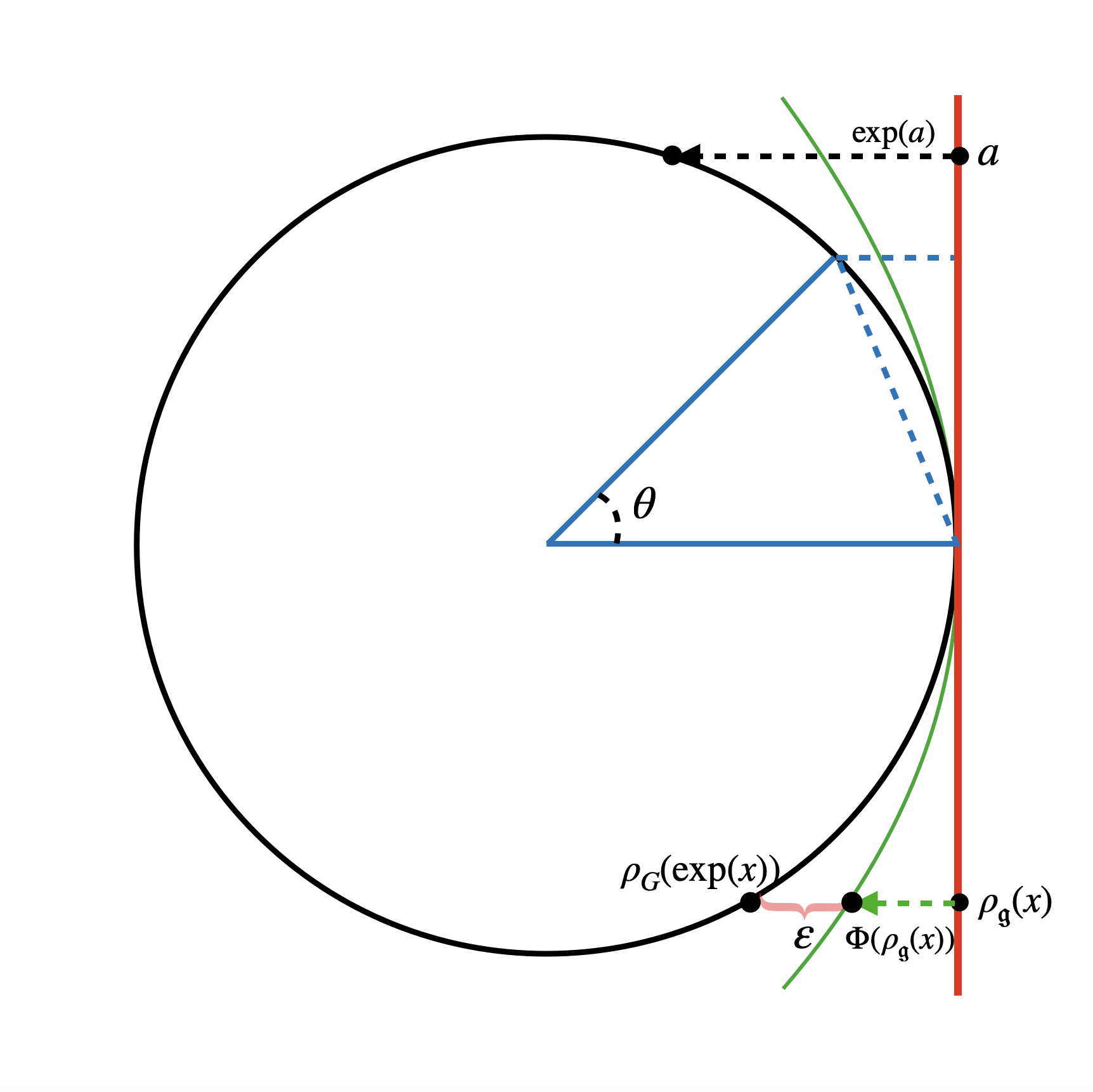
Recently, the equivariance of models with respect to a group action has become an important topic of research in machine learning. Analysis of the built-in equivariance of existing neural network architectures, as well as the study of building models that explicitly "bake in" equivariance, have become significant research areas in their own right. However, imbuing an architecture with a specific group equivariance imposes a strong prior on the types of data transformations that the model expects to see. While strictly-equivariant models enforce symmetries, real-world data does not always conform to such strict equivariances. In such cases, the prior of strict equivariance can actually prove too strong and cause models to underperform. Therefore, in this work we study a closely related topic, that of almost equivariance. We provide a definition of almost equivariance and give a practical method for encoding almost equivariance in models by appealing to the Lie algebra of a Lie group. Specifically, we define Lie algebra convolutions and demonstrate that they offer several benefits over Lie group convolutions, including being well-defined for non-compact Lie groups having non-surjective exponential map. From there, we demonstrate connections between the notions of equivariance and isometry and those of almost equivariance and almost isometry. We prove two existence theorems, one showing the existence of almost isometries within bounded distance of isometries of a manifold, and another showing the converse for Hilbert spaces. We extend these theorems to prove the existence of almost equivariant manifold embeddings within bounded distance of fully equivariant embedding functions, subject to certain constraints on the group action and the function class. Finally, we demonstrate the validity of our approach by benchmarking against datasets in fully equivariant and almost equivariant settings.
翻译:暂无翻译