Dimension Reduction and Data Visualization for Fréchet Regression

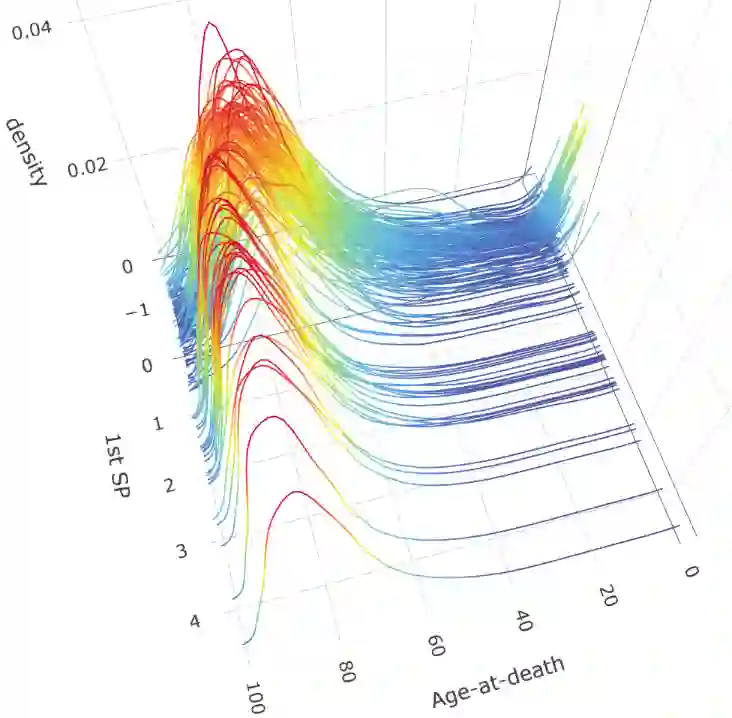
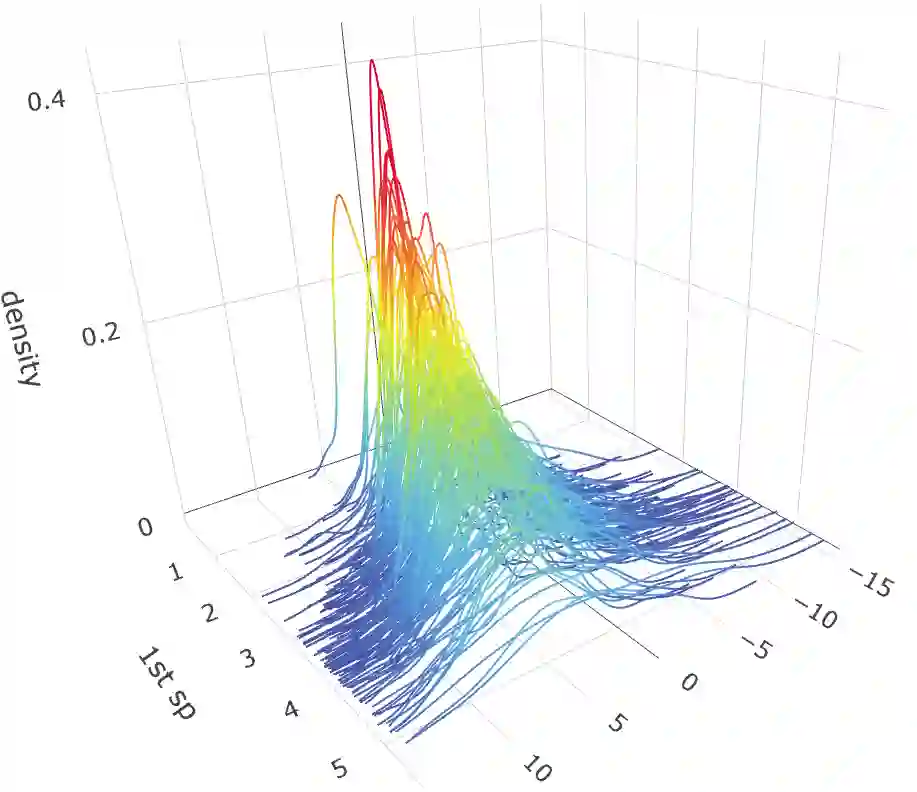
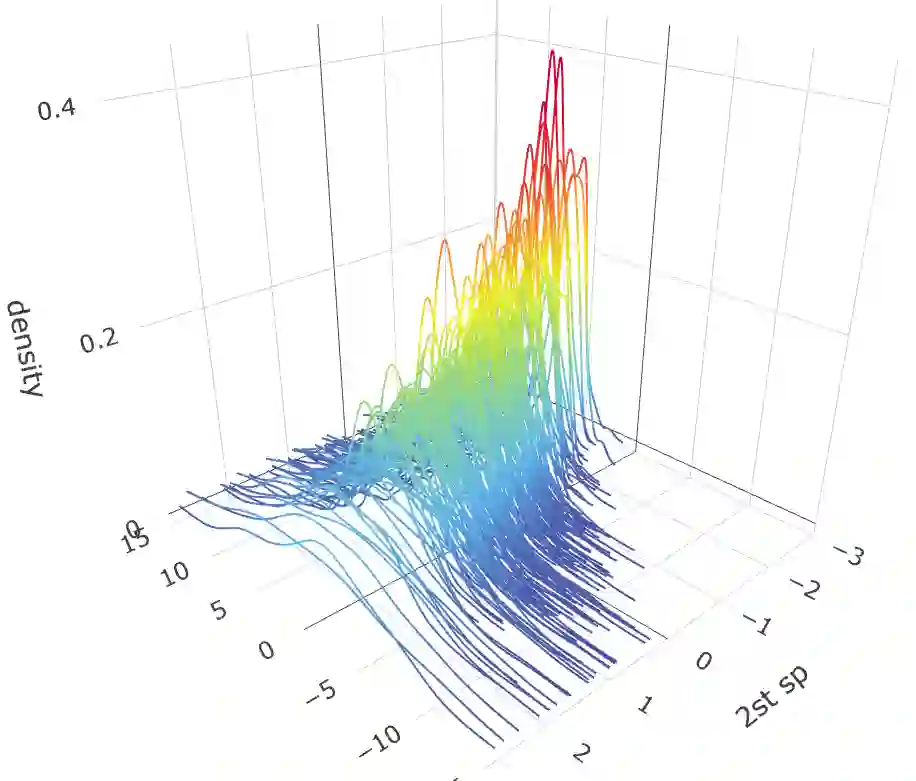
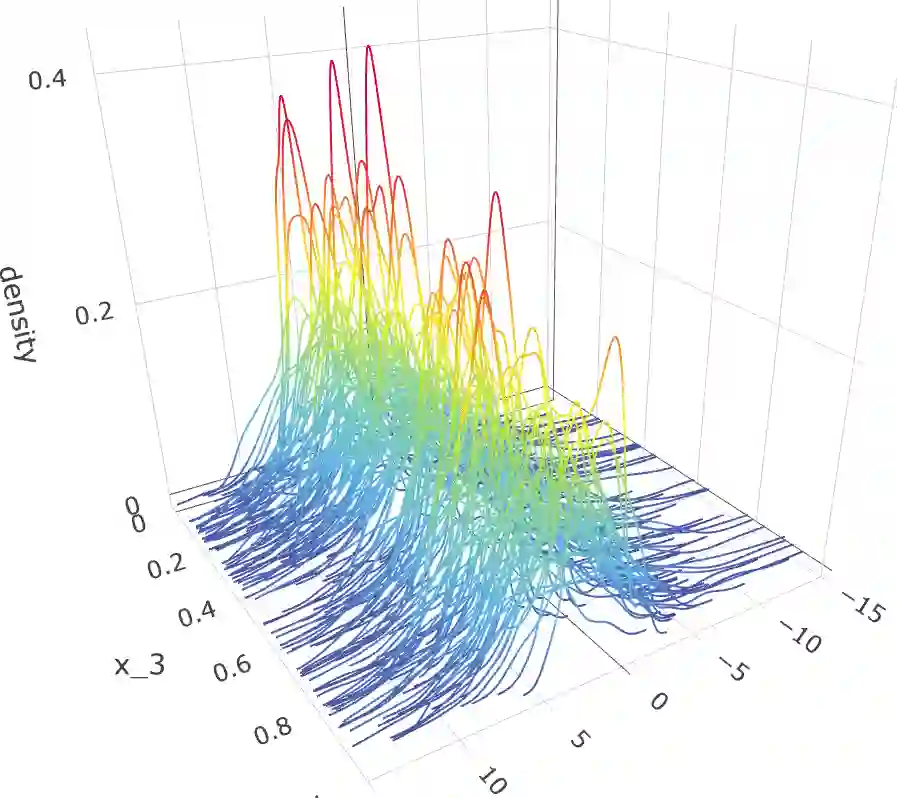
With the rapid development of data collection techniques, complex data objects that are not in the Euclidean space are frequently encountered in new statistical applications. Fr\'echet regression model (Peterson & M\"uller 2019) provides a promising framework for regression analysis with metric space-valued responses. In this paper, we introduce a flexible sufficient dimension reduction (SDR) method for Fr\'echet regression to achieve two purposes: to mitigate the curse of dimensionality caused by high-dimensional predictors, and to provide a tool for data visualization for Fr\'echet regression. Our approach is flexible enough to turn any existing SDR method for Euclidean (X,Y) into one for Euclidean X and metric space-valued Y. The basic idea is to first map the metric-space valued random object $Y$ to a real-valued random variable $f(Y)$ using a class of functions, and then perform classical SDR to the transformed data. If the class of functions is sufficiently rich, then we are guaranteed to uncover the Fr\'echet SDR space. We showed that such a class, which we call an ensemble, can be generated by a universal kernel. We established the consistency and asymptotic convergence rate of the proposed methods. The finite-sample performance of the proposed methods is illustrated through simulation studies for several commonly encountered metric spaces that include Wasserstein space, the space of symmetric positive definite matrices, and the sphere. We illustrated the data visualization aspect of our method by exploring the human mortality distribution data across countries and by studying the distribution of hematoma density.