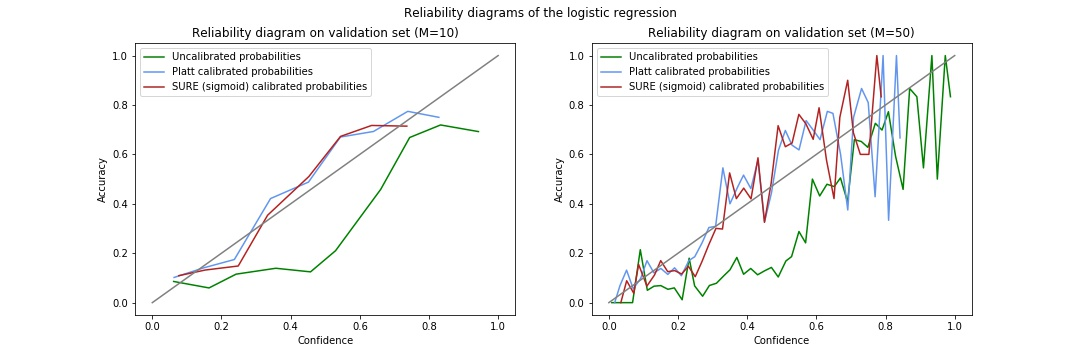
In this article we compare the performances of a logistic regression and a feed forward neural network for credit scoring purposes. Our results show that the logistic regression gives quite good results on the dataset and the neural network can improve a little the performance. We also consider different sets of features in order to assess their importance in terms of prediction accuracy. We found that temporal features (i.e. repeated measures over time) can be an important source of information resulting in an increase in the overall model accuracy. Finally, we introduce a new technique for the calibration of predicted probabilities based on Stein's unbiased risk estimate (SURE). This calibration technique can be applied to very general calibration functions. In particular, we detail this method for the sigmoid function as well as for the Kumaraswamy function, which includes the identity as a particular case. We show that stacking the SURE calibration technique with the classical Platt method can improve the calibration of predicted probabilities.
翻译:在文章中,我们为信用评分的目的比较了物流回归和前向神经网络的性能。我们的结果表明,物流回归在数据集上取得了相当好的结果,神经网络可以稍稍改善性能。我们还考虑了不同的特征组,以便评估其在预测准确性方面的重要性。我们发现,时间特征(即长期反复测量)可以成为一个重要的信息来源,从而提高总体模型准确性。最后,我们引入了一种根据斯坦的公正风险估计(SURE)对预测概率进行校准的新技术。这种校准技术可以应用到非常普遍的校准功能中。特别是,我们详细介绍了用于示意功能和库马拉斯瓦米功能的这一方法,其中包括作为特定案例的特性。我们表明,用古典普拉特方法堆放的SURS校准技术可以改进预测概率的校准。