Breaking the $f+1$ Barrier: Executing Payment Transactions in Parallel with Less than $f+1$ Validations

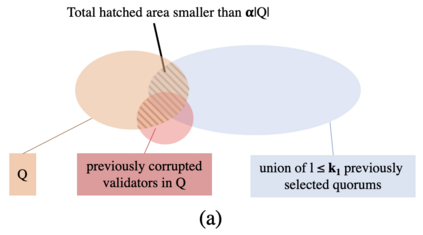
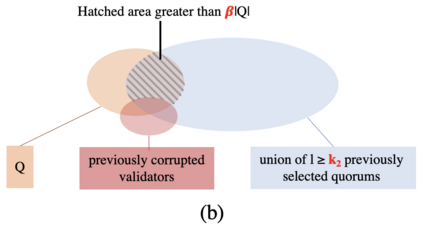
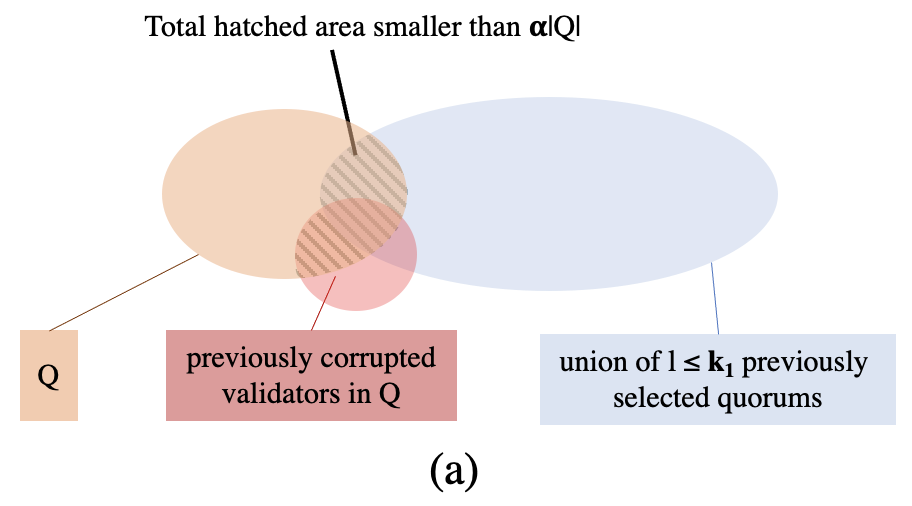
We consider the problem of supporting payment transactions in an asynchronous system in which up to $f$ validators are subject to Byzantine failures under the control of an adaptive adversary. It was shown that this problem can be solved without consensus by using byzantine quorum systems (requiring at least $2f+1$ validations per transaction in asynchronous systems). We show that it is possible to validate transactions in parallel with less than $f$ validations per transaction if each transaction spends no more that a small fraction of a balance. Our solution relies on a novel quorum system that we introduce in this paper and that we call $(k_1,k_2)$-quorum systems. In the presence of a non-adaptive adversary, these systems can be used to allow up to $k_1$ transactions to be validated concurrently and asynchronously but prevent more than $k_2$ transactions from being validated. If the adversary is adaptive, these systems can be used to allow $k_1$ transaction to be validated and prevent more than $k'_2 > k_2$ transactions from being validated, the difference $k'_2-k_2$ being dependent on the quorum system's {\em validation slack}, which we define in this paper. Using $(k_1,k_2)$-quorum systems, a payer can execute multiple partial spending transactions to spend a portion of its initial balance with less than full quorum validation (less than $f$ validations per transaction) then reclaim any remaining funds using one fully validated transaction, which we call a {\em settlement} transaction.