Computable complete invariants for finite clouds of unlabeled points under Euclidean isometry

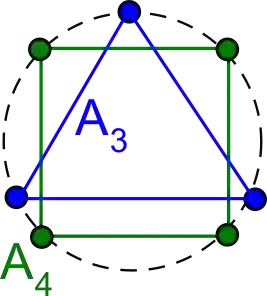
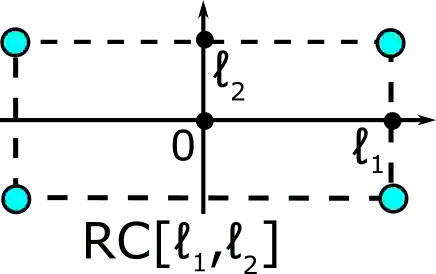A finite cloud of unlabeled points is the simplest representation of many real objects such as rigid shapes considered modulo rigid motion or isometry preserving inter-point distances. The distance matrix uniquely determines any finite cloud of labeled (ordered) points under Euclidean isometry but is intractable for comparing clouds of unlabeled points due to a huge number of permutations. The past work for unlabeled points studied the binary problem of isometry detection, incomplete invariants, or approximations to Hausdorff-style distances, which require minimizations over infinitely many general isometries. This paper introduces the first continuous and complete isometry invariants for finite clouds of unlabeled points considered under isometry in any Euclidean space. The continuity under perturbations of points in the bottleneck distance is proved in terms of new metrics that are exactly computable in polynomial time in the number of points for a fixed dimension.