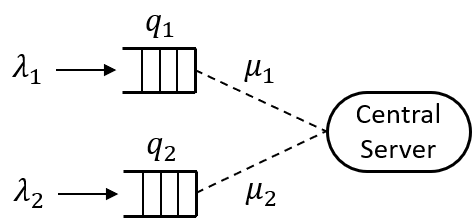
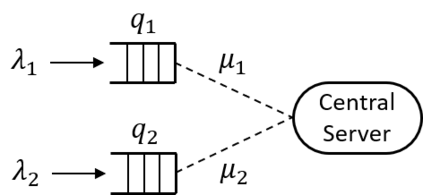
We consider the problem of reinforcement learning (RL) with unbounded state space motivated by the classical problem of scheduling in a queueing network. Traditional policies as well as error metric that are designed for finite, bounded or compact state space, require infinite samples for providing any meaningful performance guarantee (e.g. $\ell_\infty$ error) for unbounded state space. That is, we need a new notion of performance metric. As the main contribution of this work, inspired by the literature in queuing systems and control theory, we propose stability as the notion of "goodness": the state dynamics under the policy should remain in a bounded region with high probability. As a proof of concept, we propose an RL policy using Sparse-Sampling-based Monte Carlo Oracle and argue that it satisfies the stability property as long as the system dynamics under the optimal policy respects a Lyapunov function. The assumption of existence of a Lyapunov function is not restrictive as it is equivalent to the positive recurrence or stability property of any Markov chain, i.e., if there is any policy that can stabilize the system then it must possess a Lyapunov function. And, our policy does not utilize the knowledge of the specific Lyapunov function. To make our method sample efficient, we provide an improved, sample efficient Sparse-Sampling-based Monte Carlo Oracle with Lipschitz value function that may be of interest in its own right. Furthermore, we design an adaptive version of the algorithm, based on carefully constructed statistical tests, which finds the correct tuning parameter automatically.
翻译:我们考虑的是强化学习问题(RL),其不受约束的状态空间是由排队网络的典型排队问题驱动的。传统政策以及针对有限、封闭或紧凑状态空间设计的错误度量,需要无限的样本,为无约束状态空间提供任何有意义的性能保障(例如$@ell ⁇ infty$错误),也就是说,我们需要一个新的性能衡量概念。由于在排队系统和控制理论中的文献启发下,这项工作的主要贡献是“良好”的概念:政策下的国家动态应该保留在一个受约束、受约束或紧凑状态空间的精选区域。作为概念的证明,我们提出使用基于Sprass-Sampinging-Monte Carlo Oracle的RLLLLL政策,并主张只要最佳政策下的系统动态尊重Lyapunov的功能,它就能够满足稳定性属性。Lyapunov功能的存在并不具有限制性,因为它相当于任何Markov链的正值复现或稳定性,也就是说,如果有任何政策能够稳定系统的精度,那么,我们可以用一个基于Lypov的精度的精度的精度的精度的精度测试,那么,那么,我们就可以使用一个精度的精度的精度的精度的精度的精度测试功能。