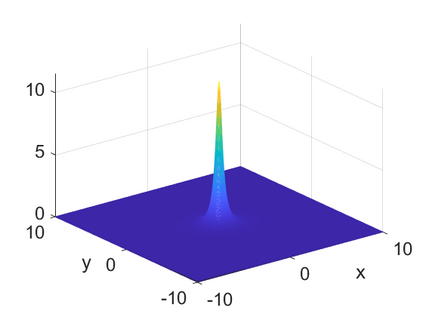
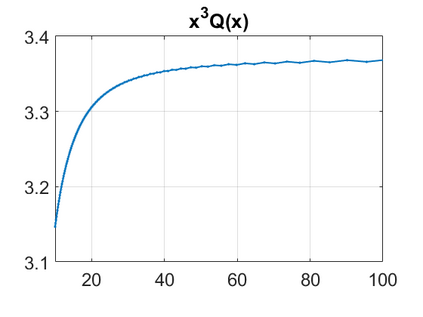
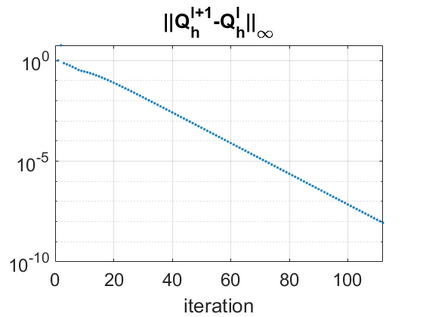
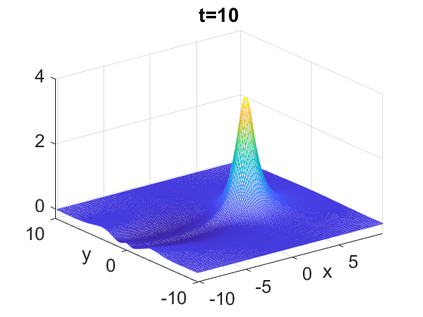
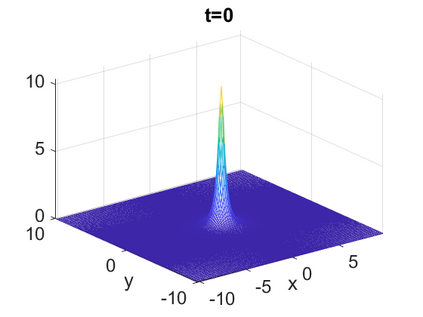
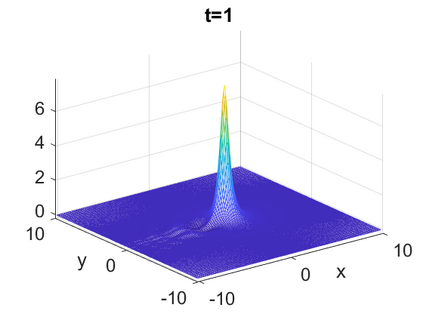
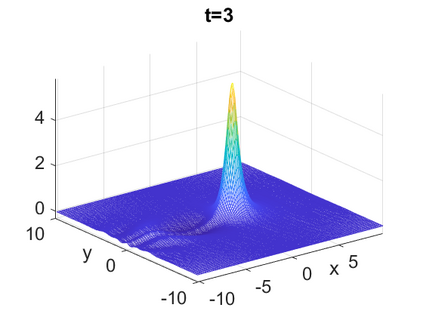
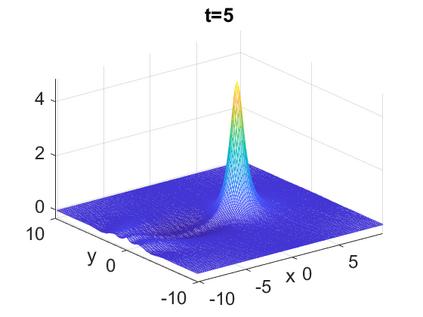
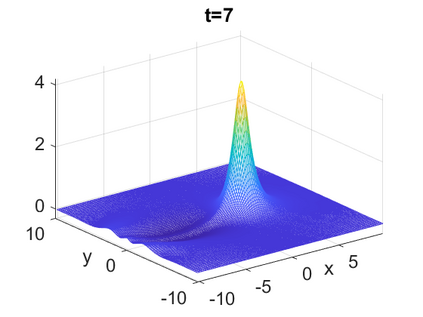
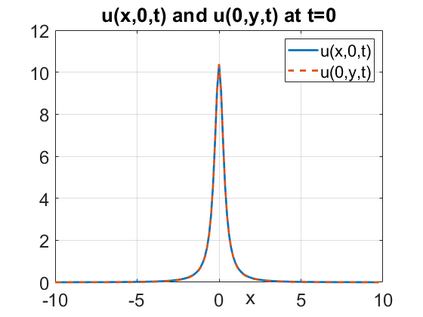
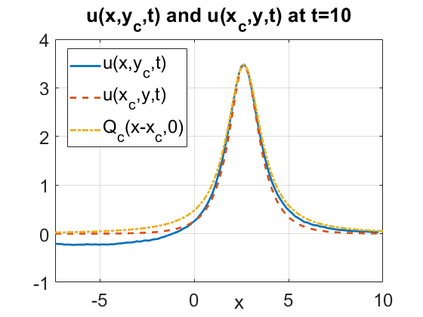
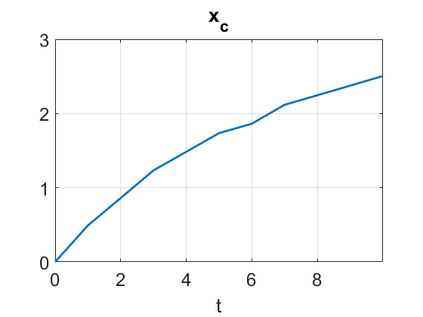
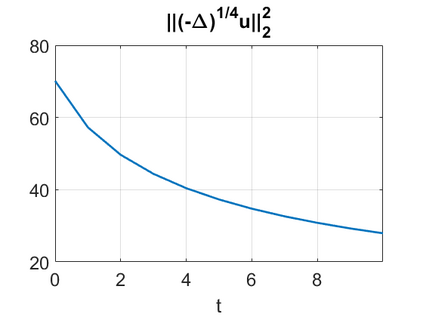
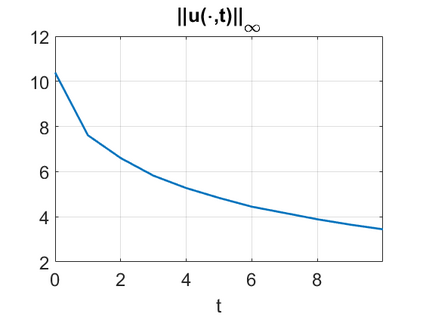
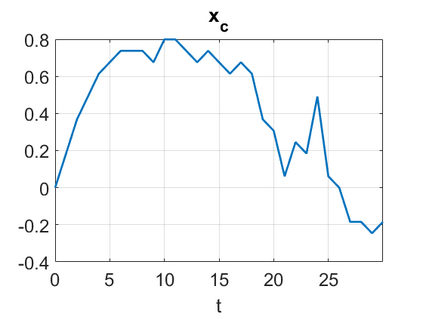
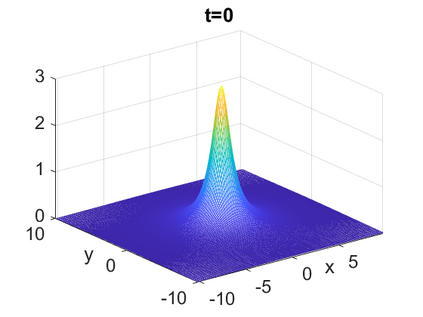
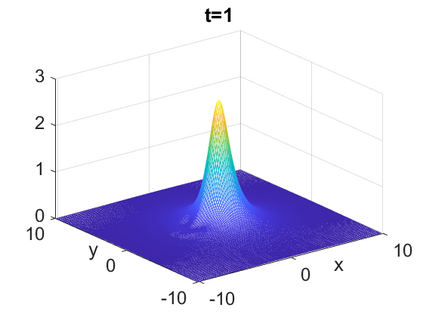
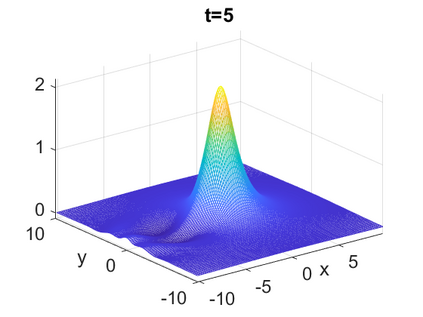
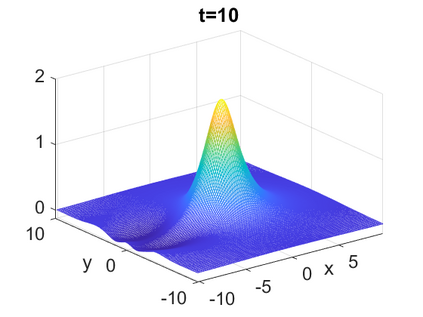
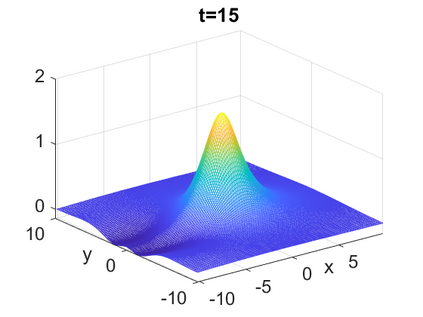
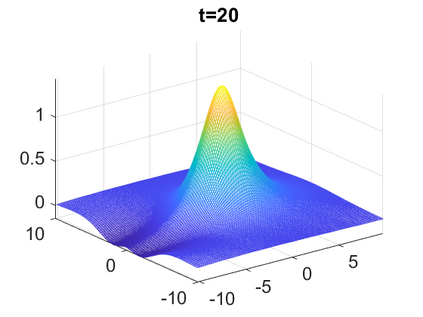
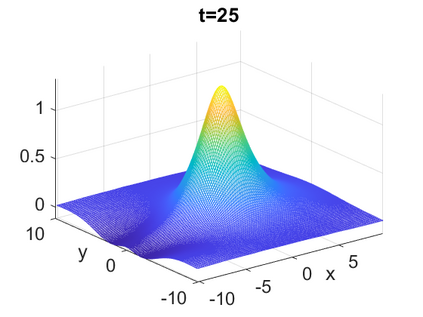
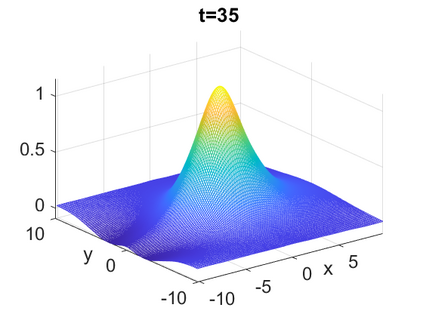
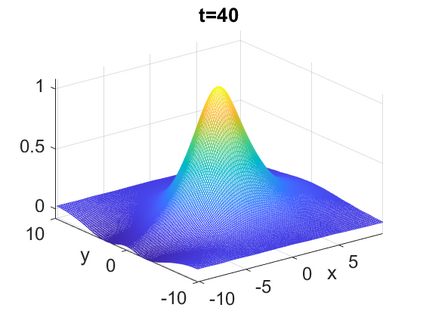
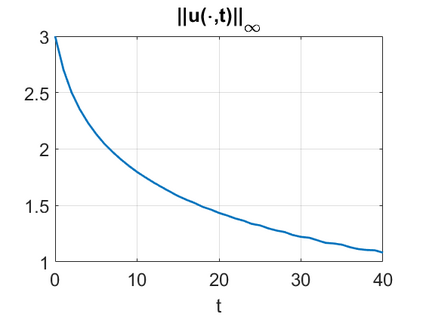
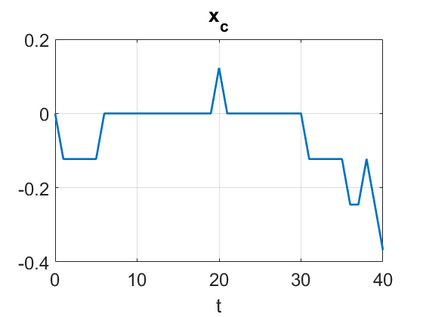
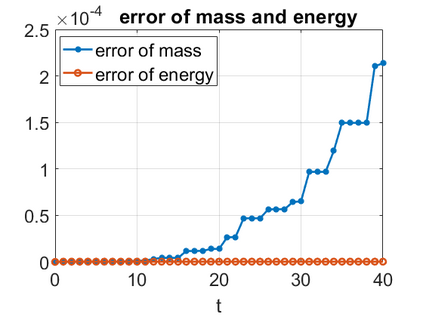
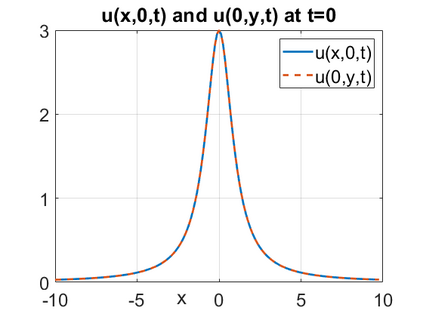
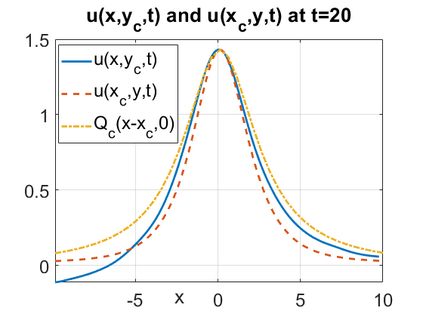
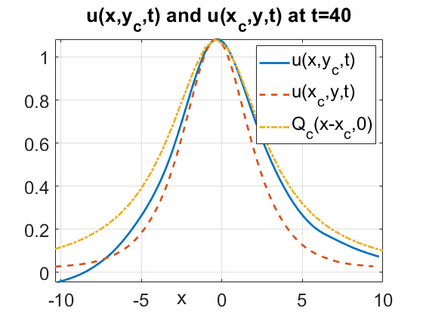
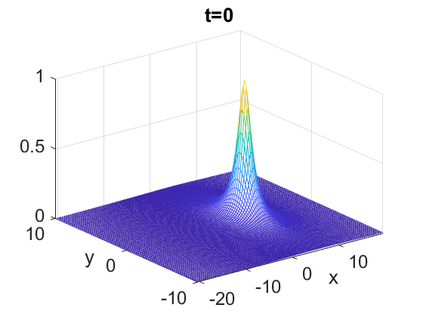
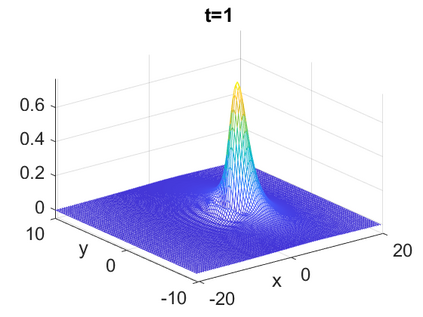
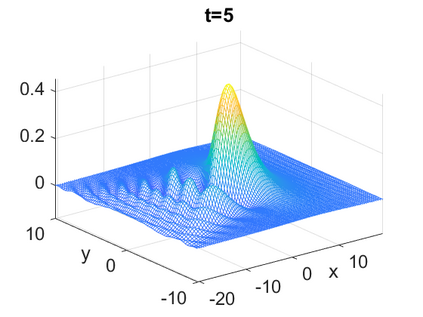
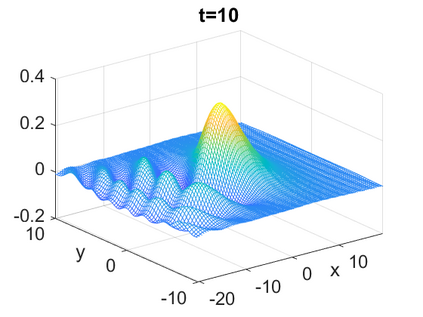
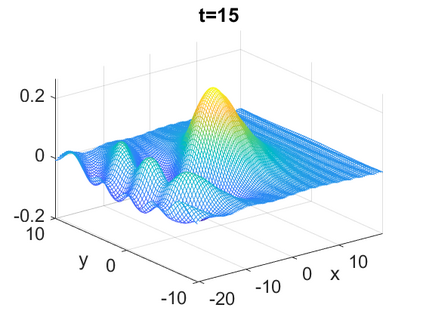
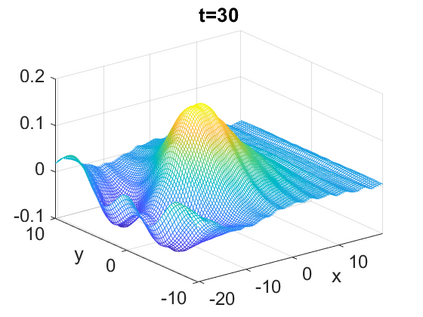
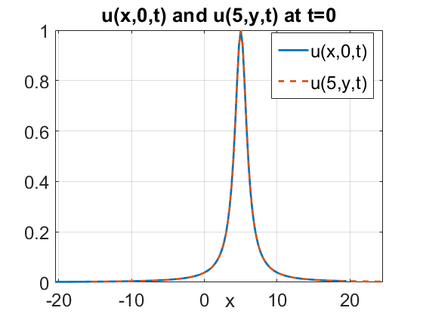
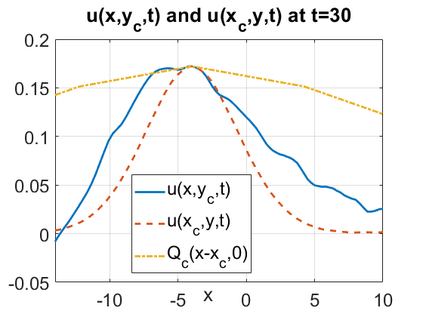
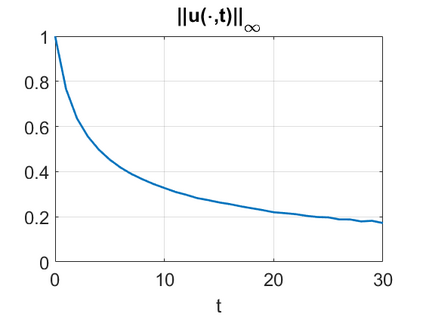
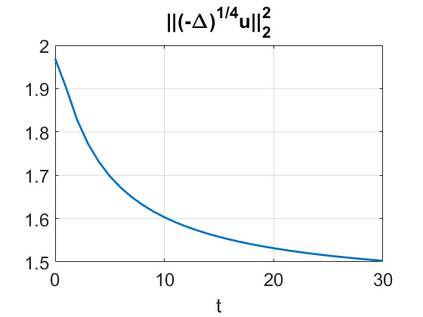
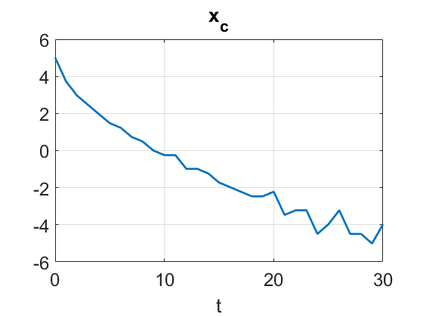
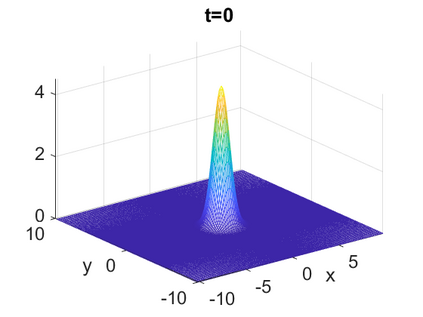
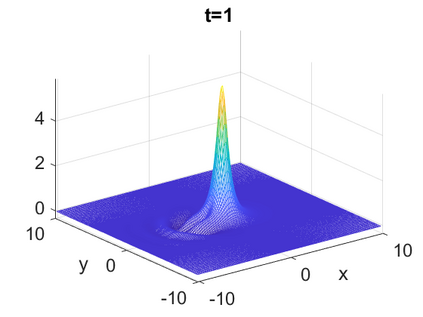
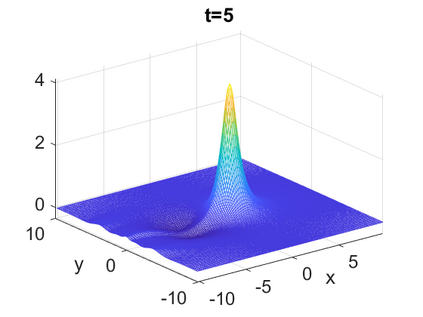
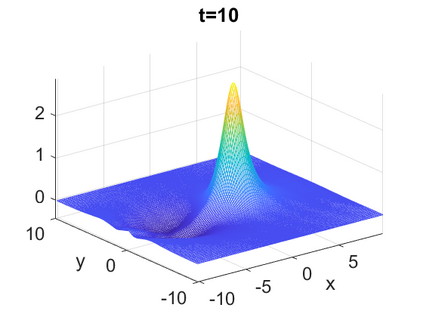
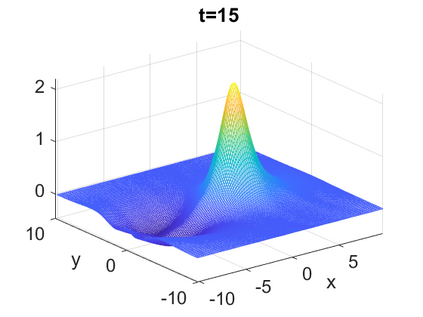
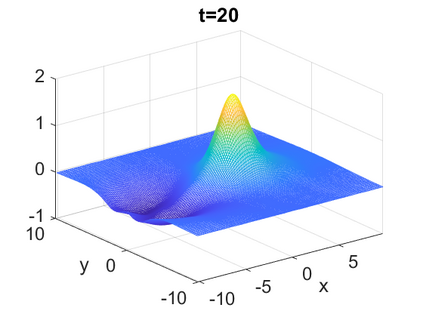
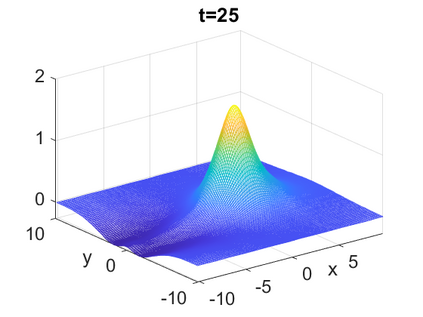
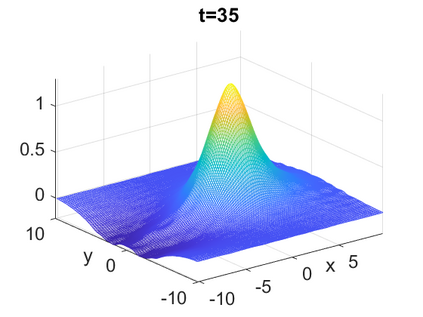
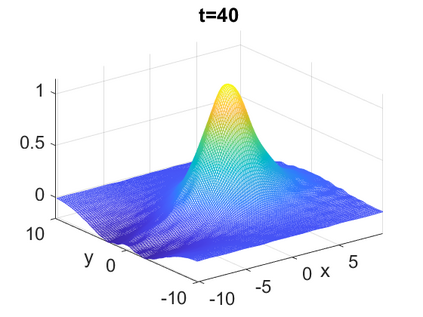
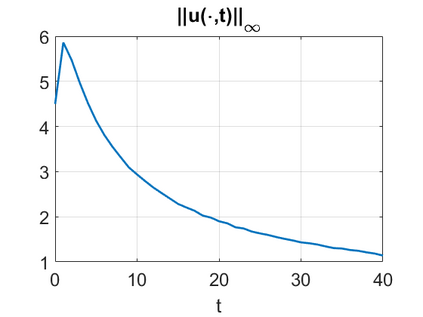
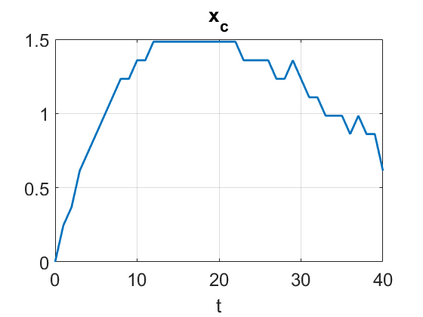
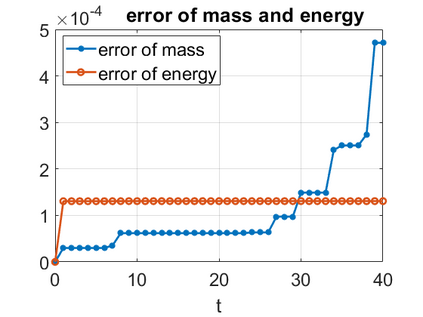
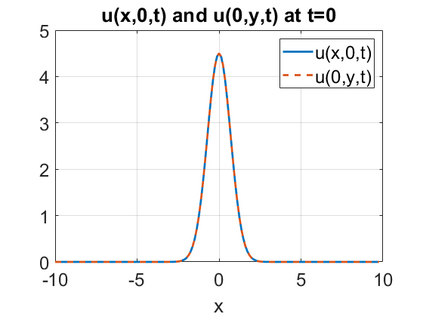
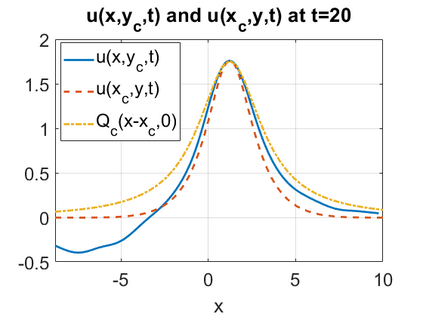
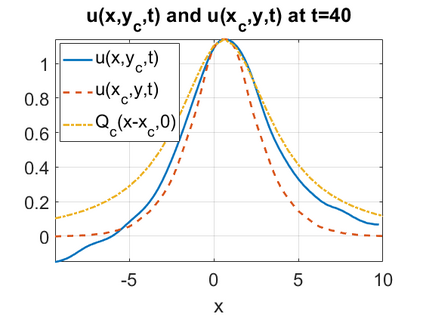
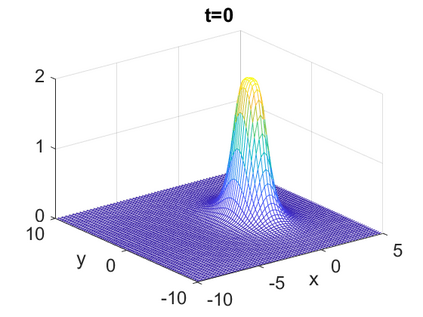
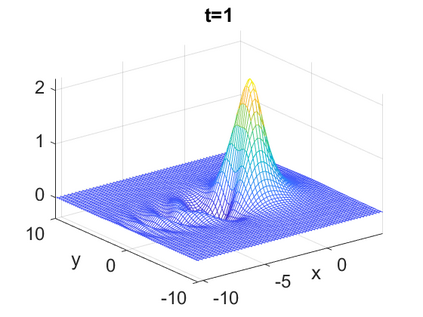
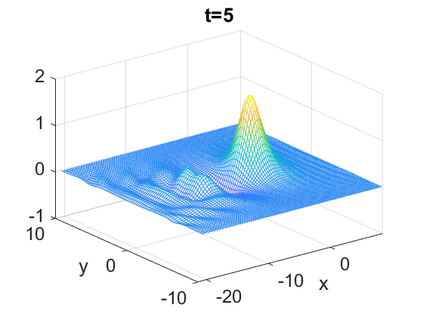
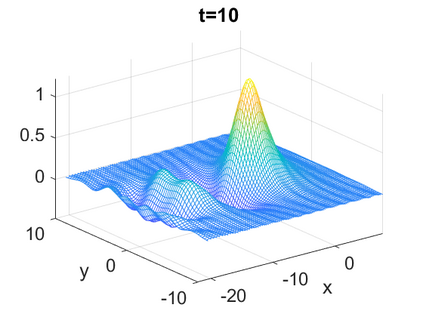
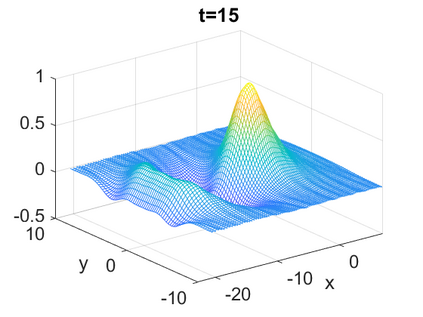
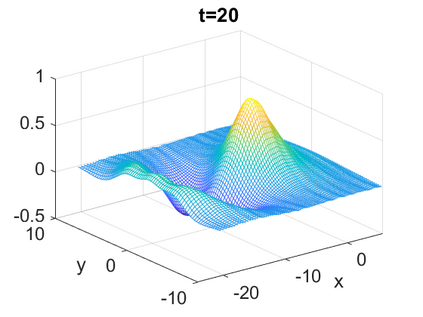
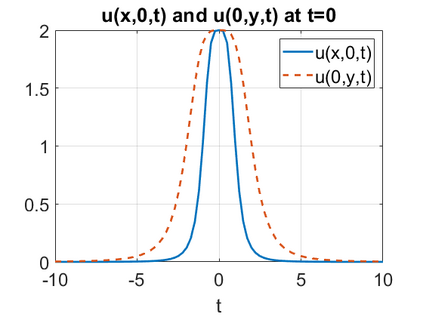
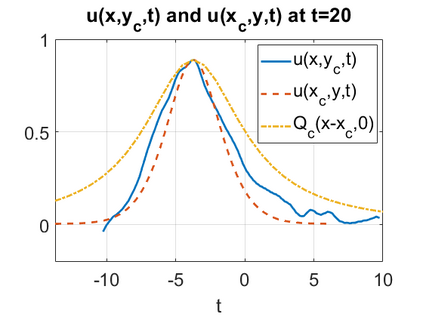
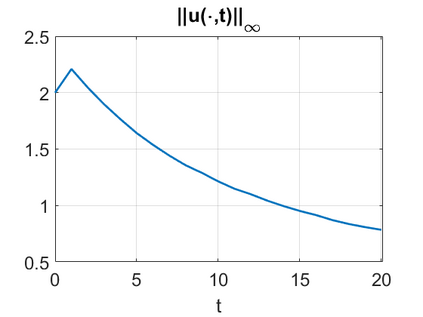
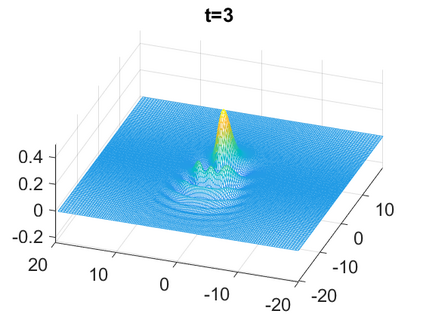
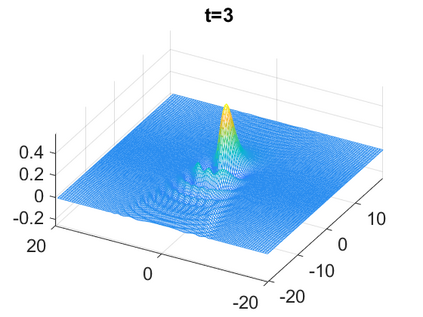
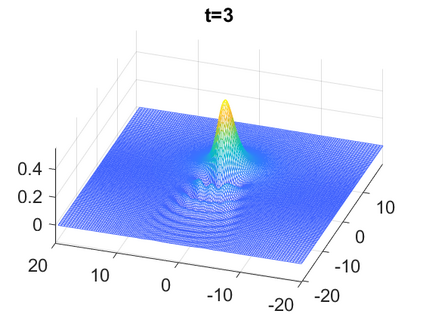
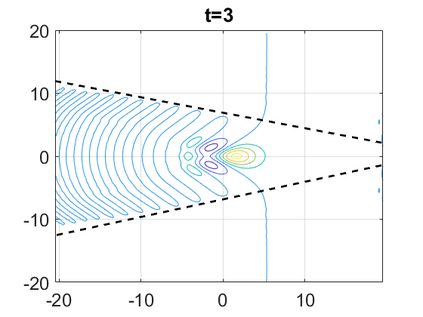
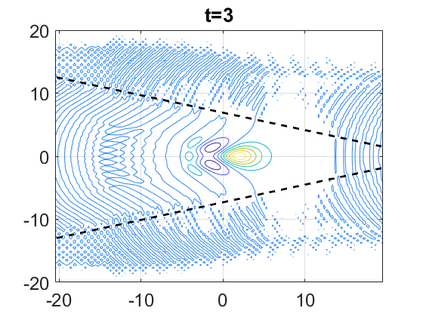
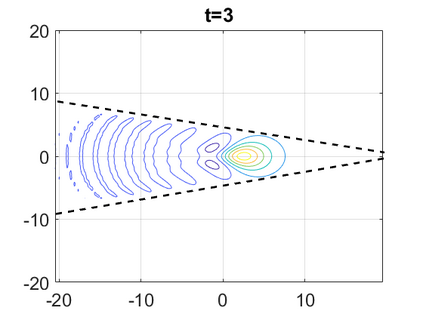
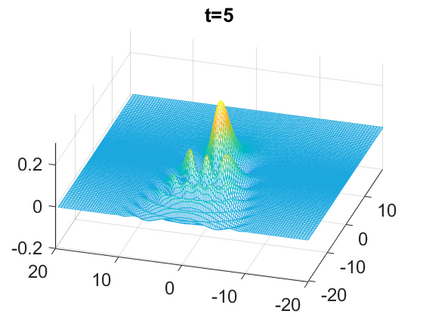
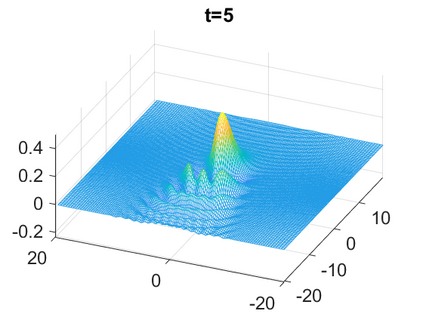
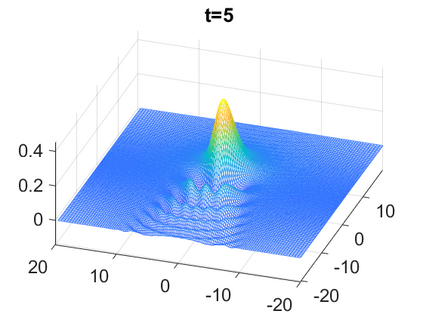
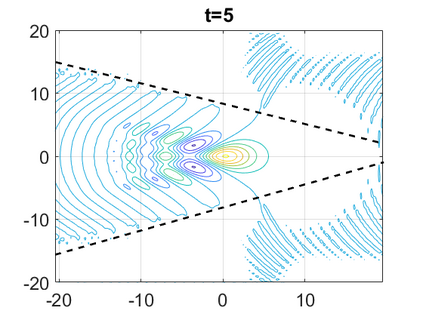
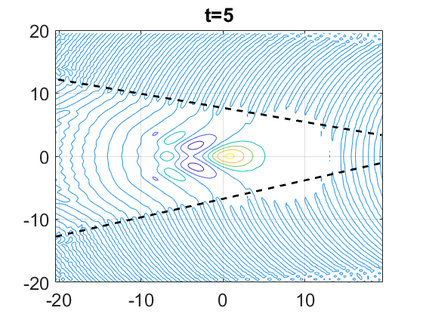
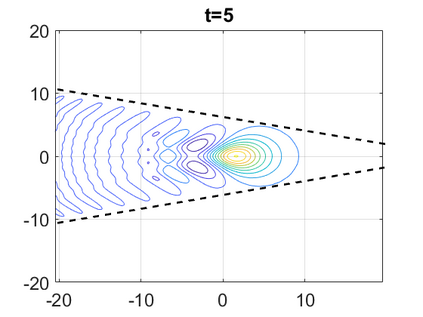
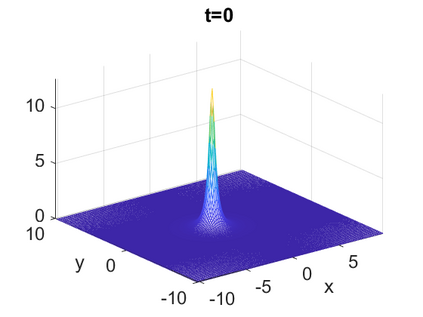
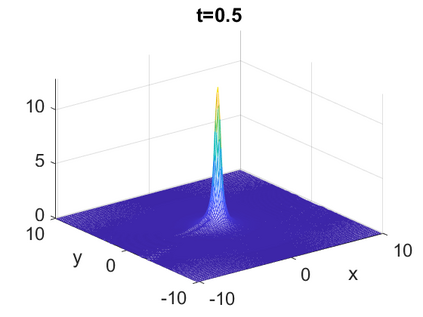
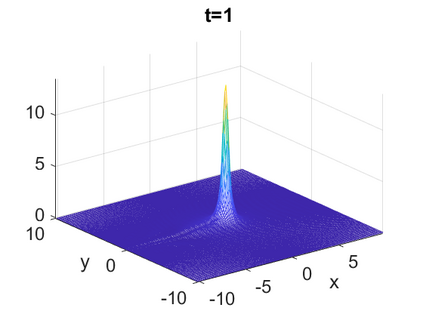
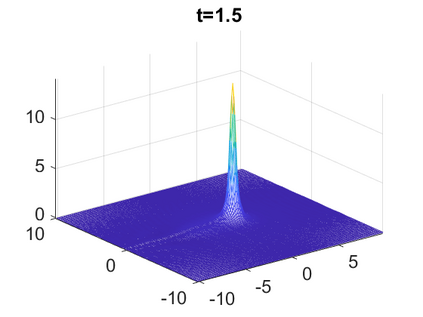
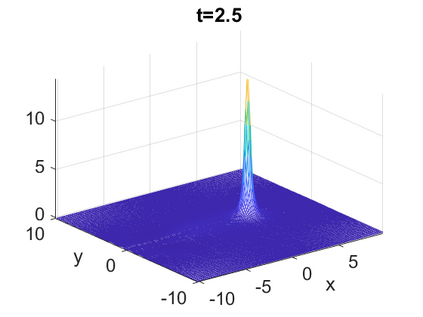
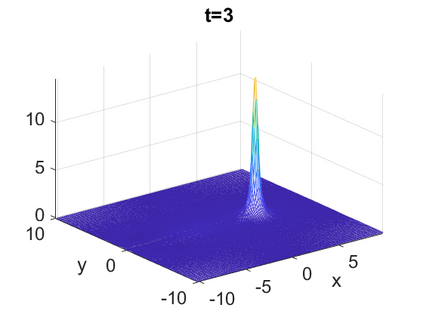
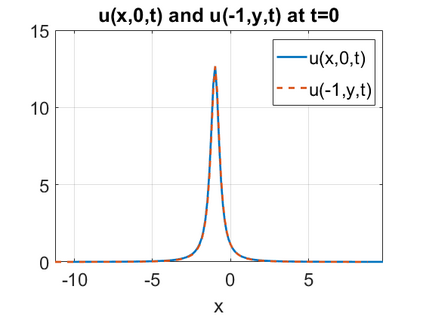
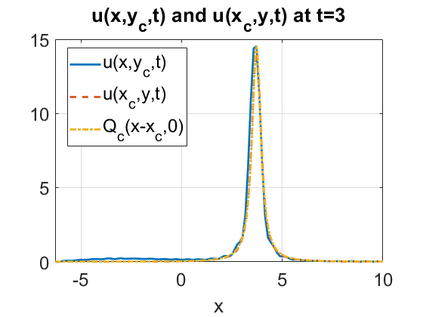
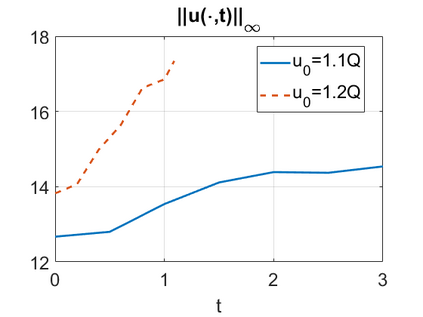
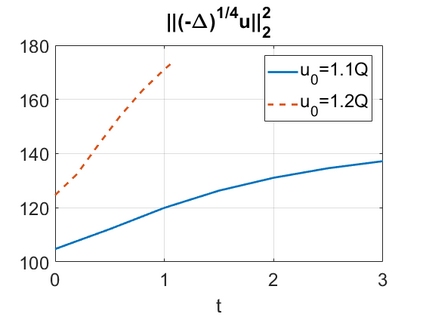
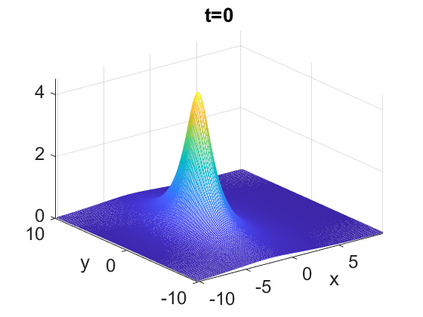
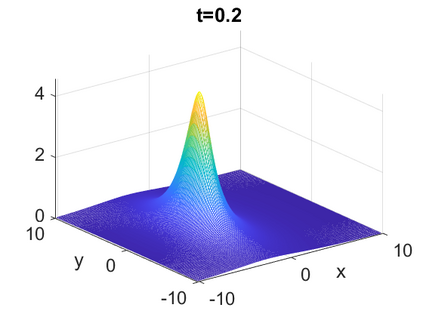
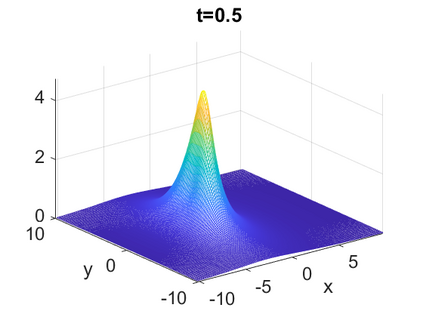
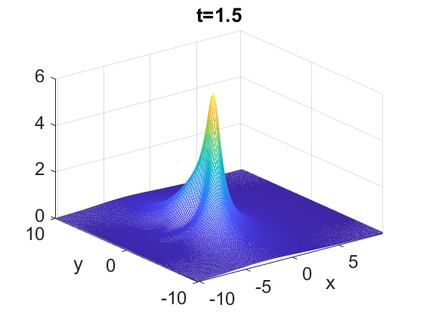
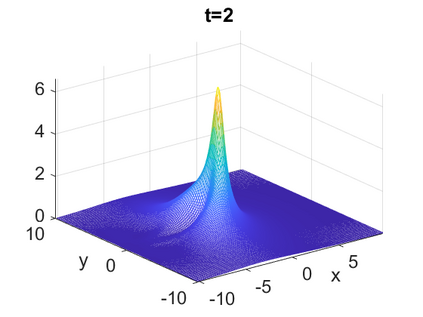
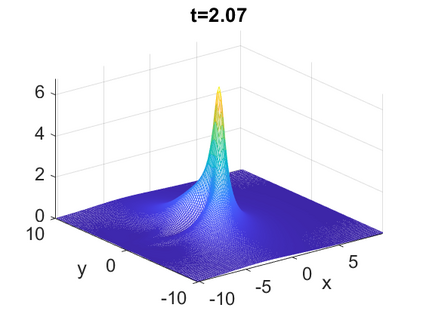
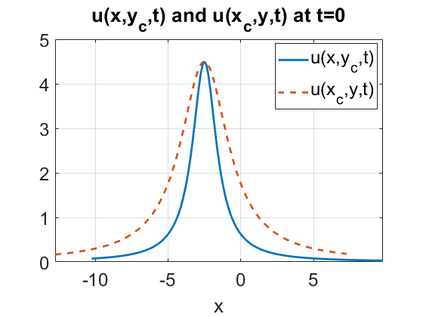
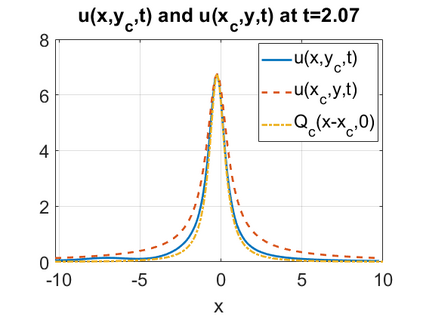
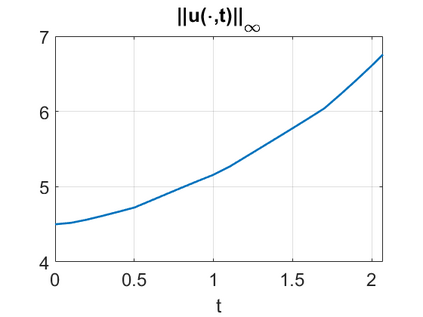
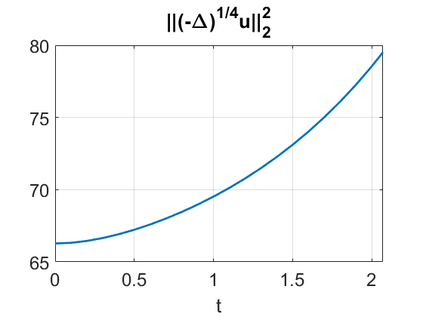
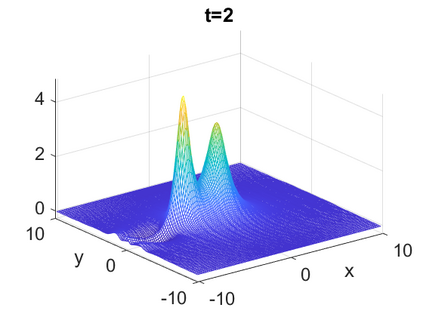
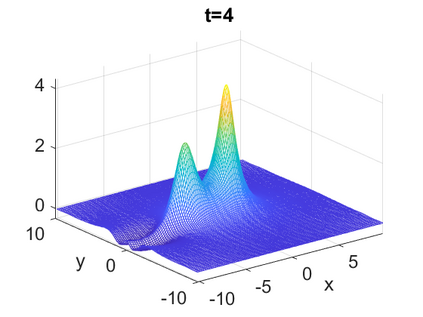
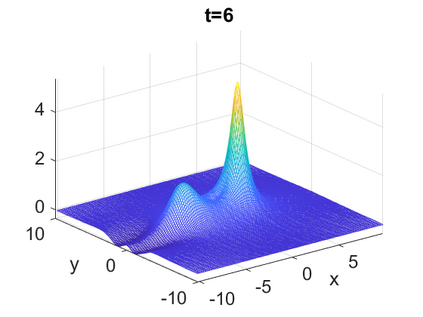
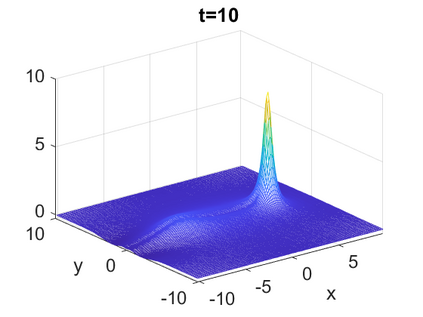
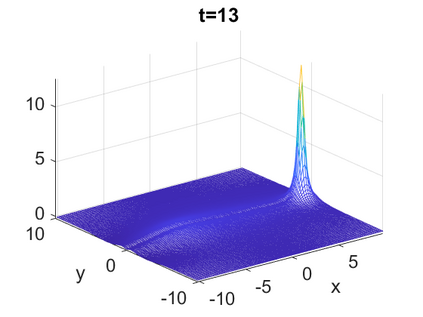
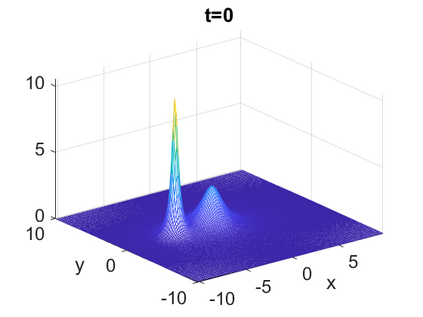
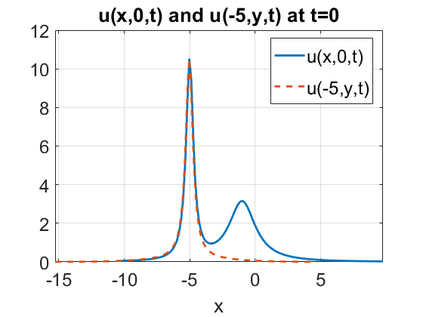
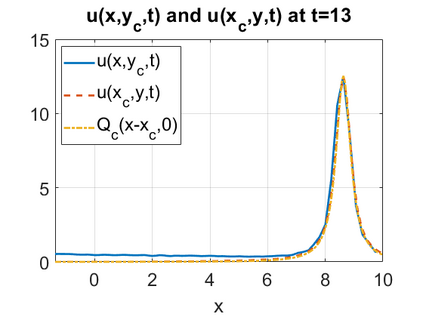
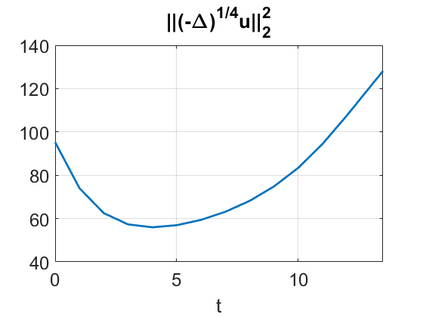
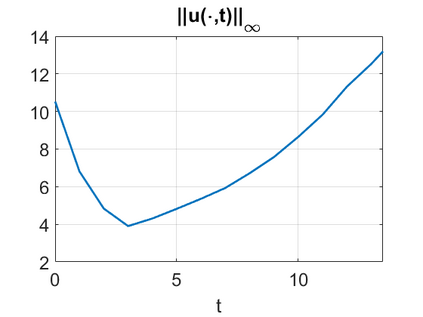
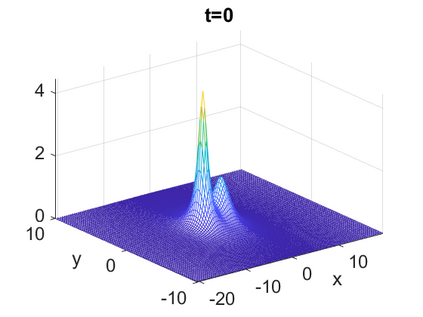
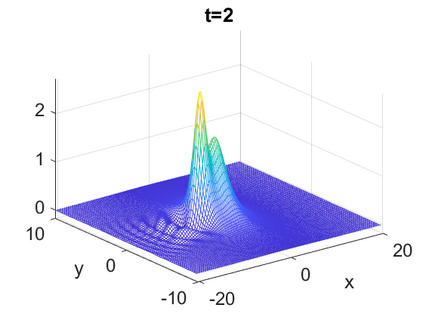
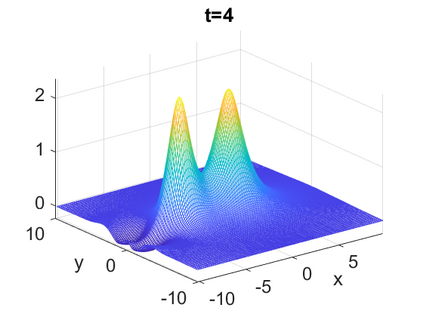
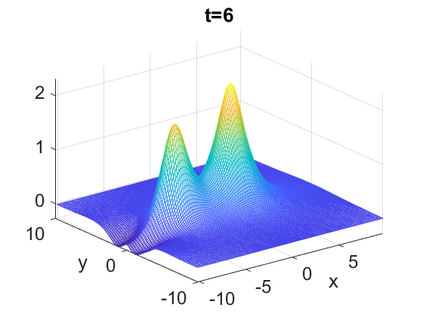
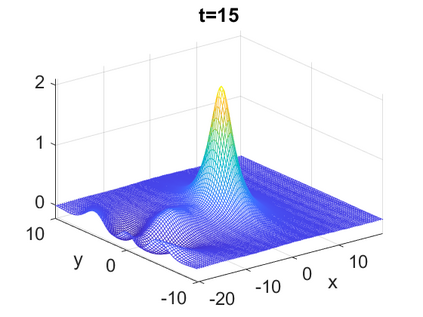
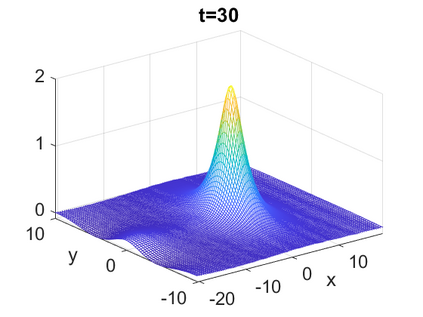
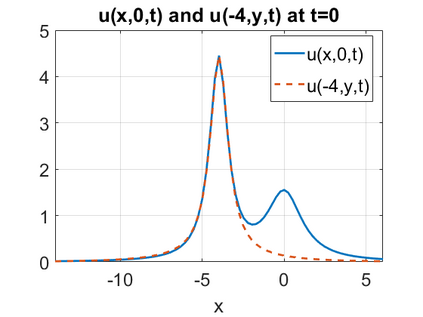
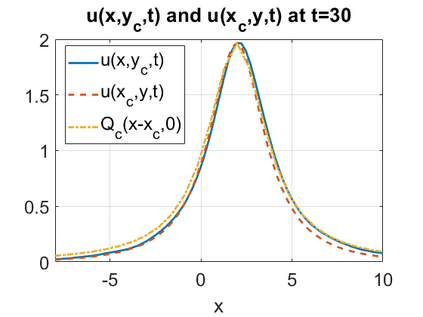
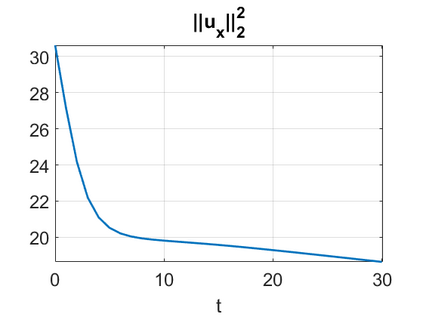
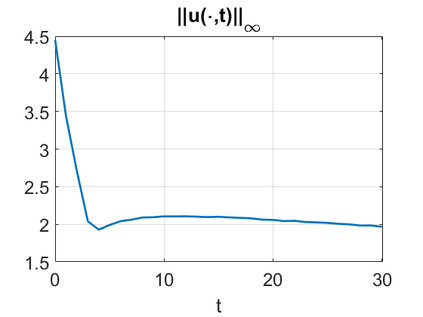
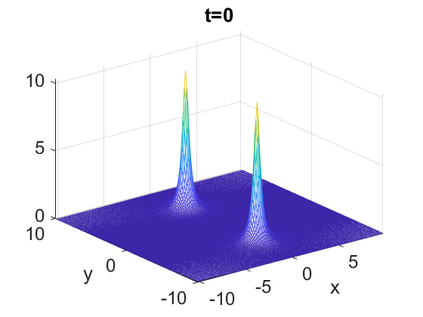
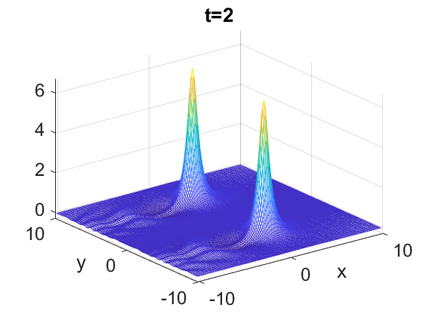
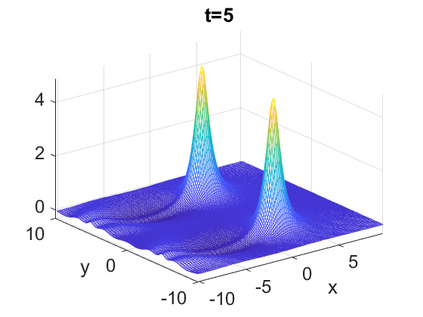
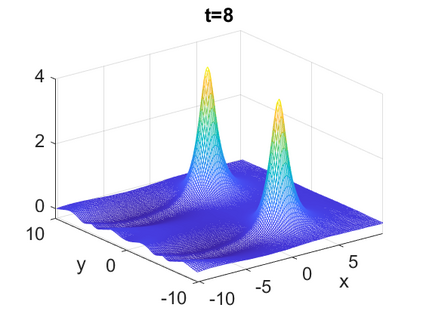
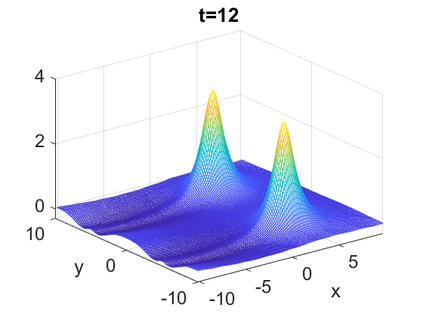
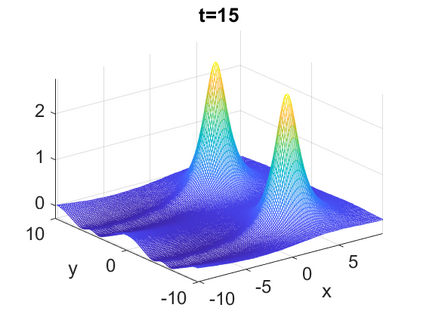
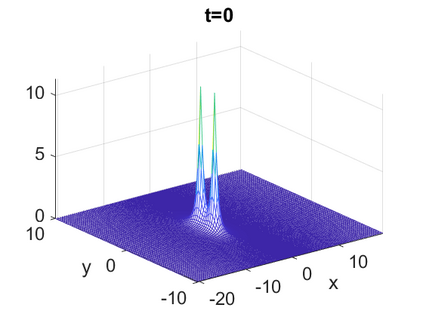
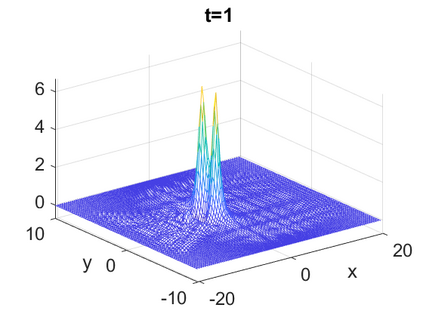
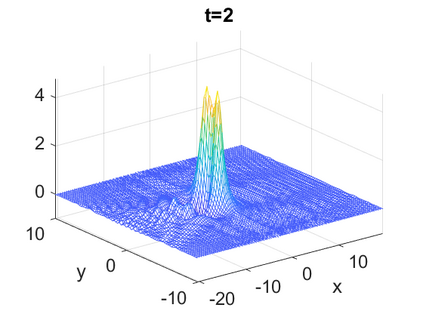
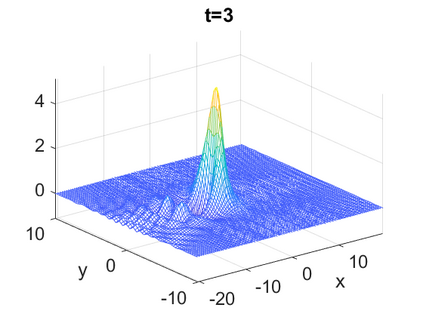
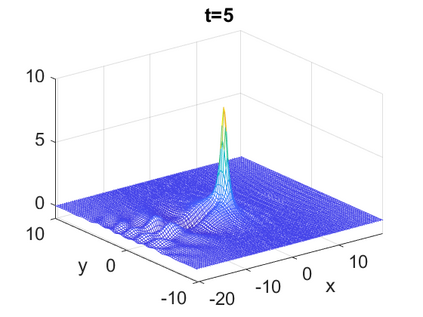
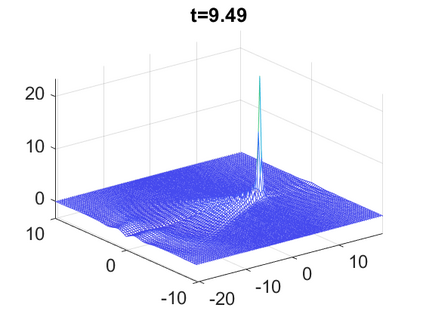
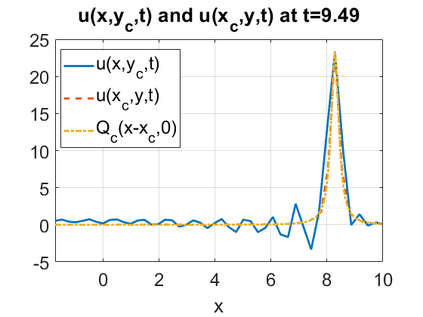
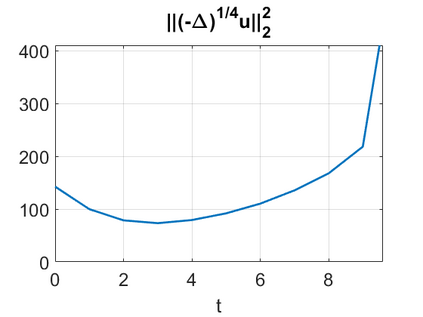
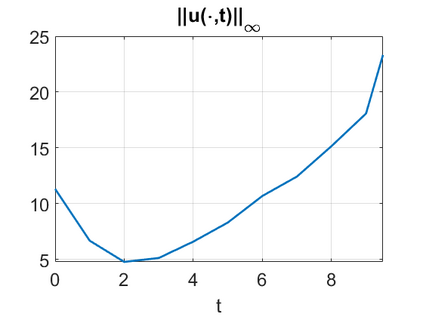
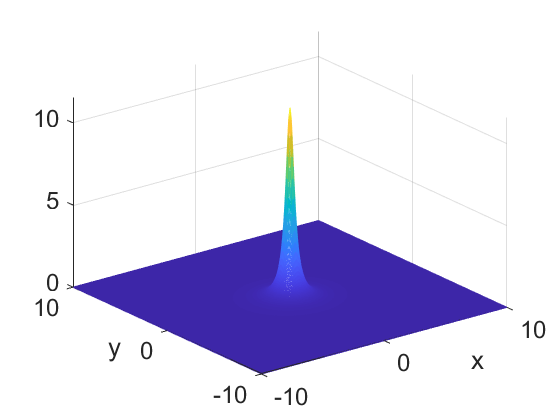
We consider a higher-dimensional version of the Benjamin-Ono (HBO) equation in the 2D setting: $u_t- \mathcal{R}_1 \Delta u + \frac{1}{2}(u^2)_x=0, (x,y) \in \mathbb{R}^2$, which is $L^2$-critical, and investigate properties of solutions both analytically and numerically. For a generalized equation (fractional 2D gKdV) after deriving the Pohozaev identities, we obtain non-existence conditions for solitary wave solutions, then prove uniform bounds in the energy space or conditional global existence, and investigate the radiation region, a specific wedge in the negative $x$-direction. We then introduce our numerical approach in a general context, and apply it to obtain the ground state solution in the 2D critical HBO equation, then show that its mass is a threshold for global vs. finite time existing solutions, which is typical in the focusing (mass-)critical dispersive equations. We also observe that globally existing solutions tend to disperse completely into the radiation in this nonlocal equation. The blow-up solutions travel in the positive $x$-direction with the rescaled ground state profile while also radiating dispersive oscillations into the radiative wedge. We conclude with examples of different interactions of two solitary wave solutions, including weak and strong interactions.
翻译:我们考虑在 2D 设置中, Benjamin- Ono (HBO) 等式的较高维度版本是 $_t- mathcal{R ⁇ 1\\\ Delta u +\ frac{1\\2} (u2)_x=0, (x,y)\ in\ mathbbb{R ⁇ 2$}R ⁇ 2$, 以分析方式和数字方式来调查解决方案的特性。 对于得出 Pohozaev 身份后的一般等式( 折射 2D gKdV ), 我们获得单波萨耶夫 单波萨耶夫 溶液的不存在条件, 然后证明在能源空间或有条件的全球存在中存在统一界限, 并且调查辐射区域, 负值为负值 $x 0. 2, 然后在2D 关键 HBO 等式中应用我们的数字方法来获得地面解决方案, 然后显示其质量是全球的临界值, 和微波波的定时现有解决方案, 典型的焦点( 临界的坚固不透度的) 和偏差的对等式方程式, 我们观察全球的平流的平流的平面的平面的平面的平面的平面的平面的平面的平面的方程式, 。