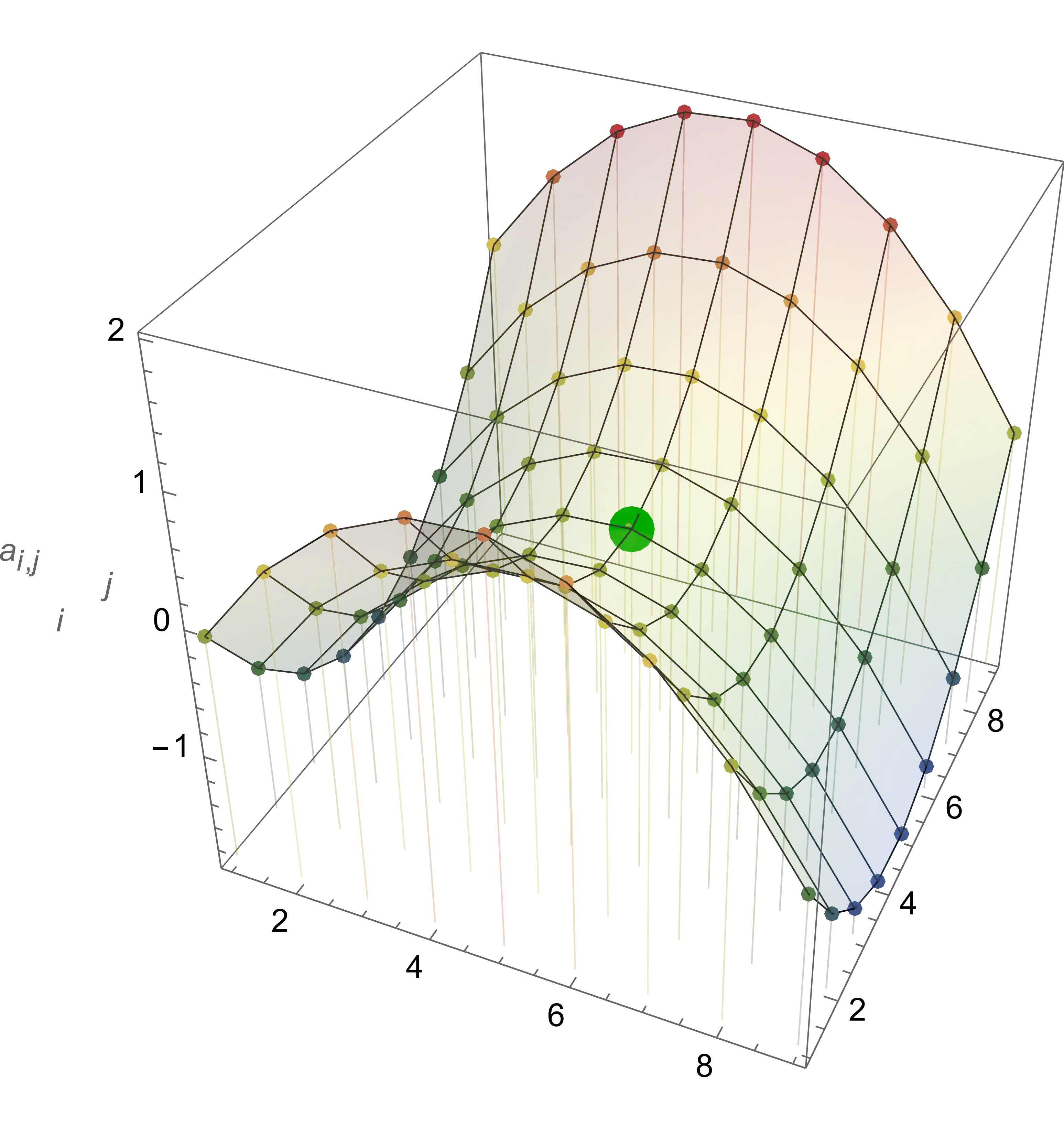
A saddlepoint of an $n \times n$ matrix $A$ is an entry of $A$ that is a maximum in its row and a minimum in its column. Knuth (1968) gave several different algorithms for finding a saddlepoint. The worst-case running time of these algorithms is $\Theta(n^2)$, and Llewellyn, Tovey, and Trick (1988) showed that this cannot be improved, as in the worst case all entries of A may need to be queried. A strict saddlepoint of $A$ is an entry that is the strict maximum in its row and the strict minimum in its column. The strict saddlepoint (if it exists) is unique, and Bienstock, Chung, Fredman, Sch\"affer, Shor, and Suri (1991) showed that it can be found in time $O(n \log{n})$, where a dominant runtime contribution is sorting the diagonal of the matrix. This upper bound has not been improved since 1991. In this paper we show that the strict saddlepoint can be found in $O(n \log^{*}{n})$ time, where $\log^{*}$ denotes the very slowly growing iterated logarithm function, coming close to the lower bound of $\Omega(n)$. In fact, we can also compute, within the same runtime, the value of a non-strict saddlepoint, assuming one exists. Our algorithm is based on a simple recursive approach, a feasibility test inspired by searching in sorted matrices, and a relaxed notion of saddlepoint.
翻译:暂无翻译