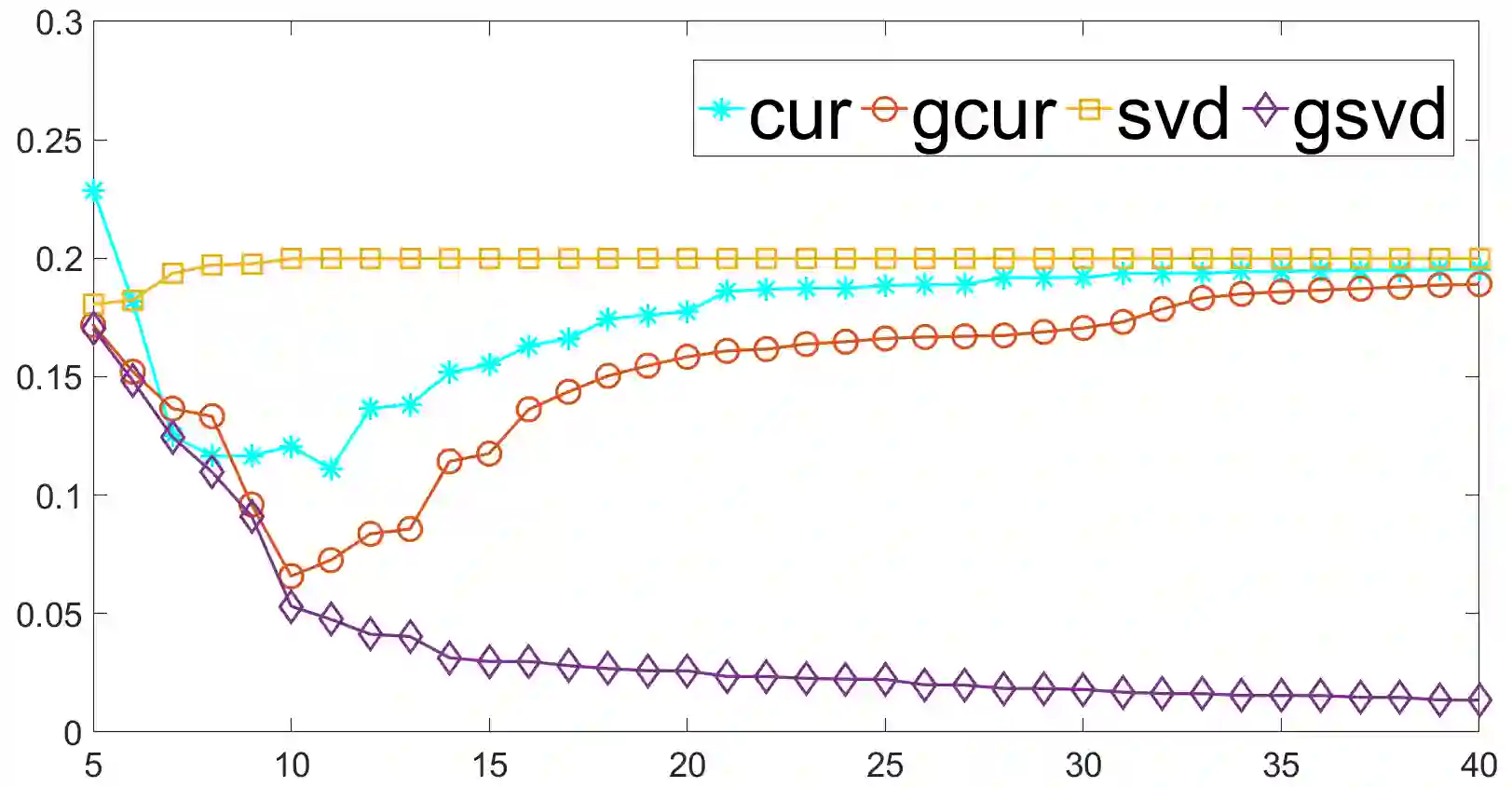
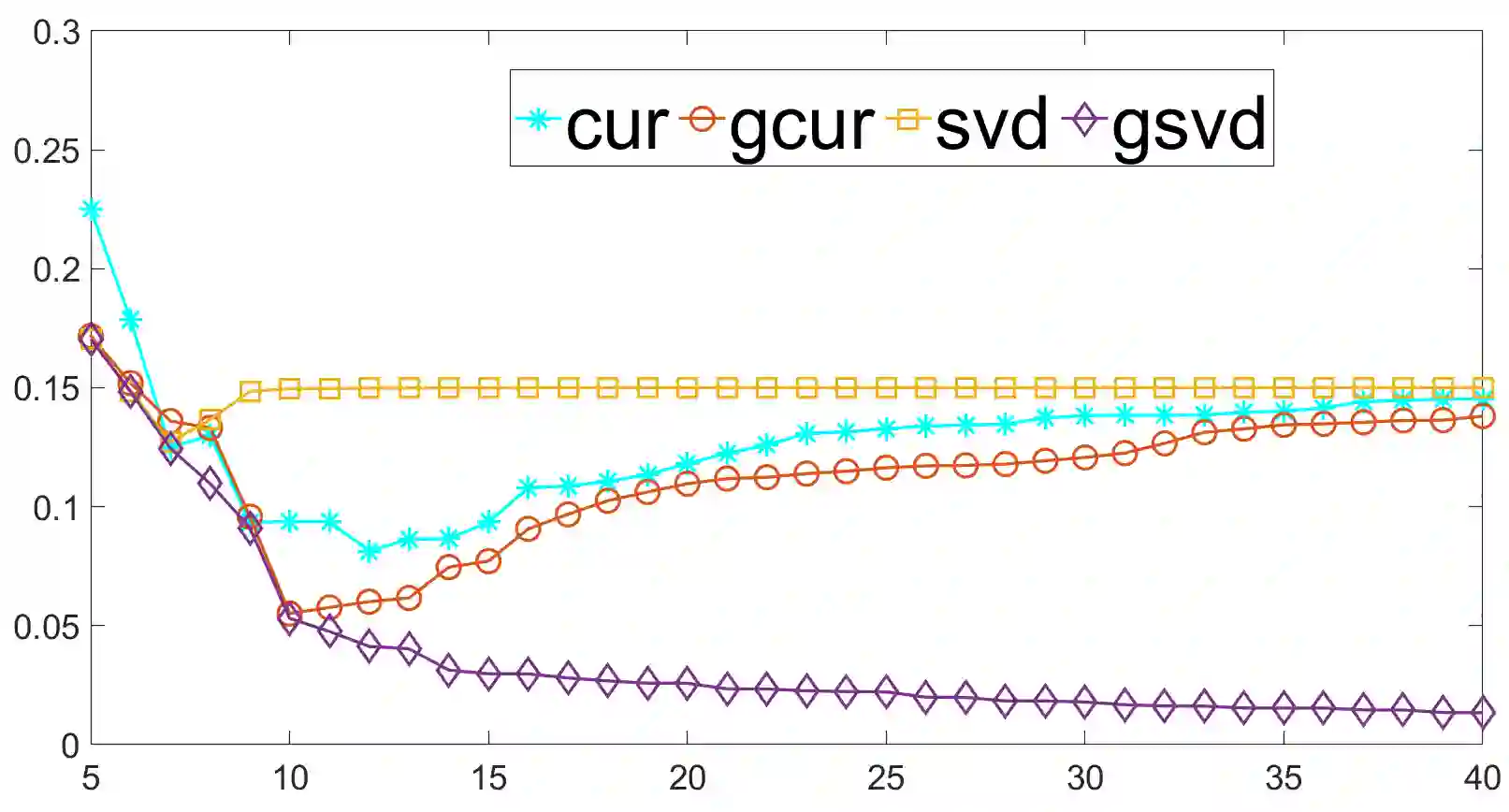
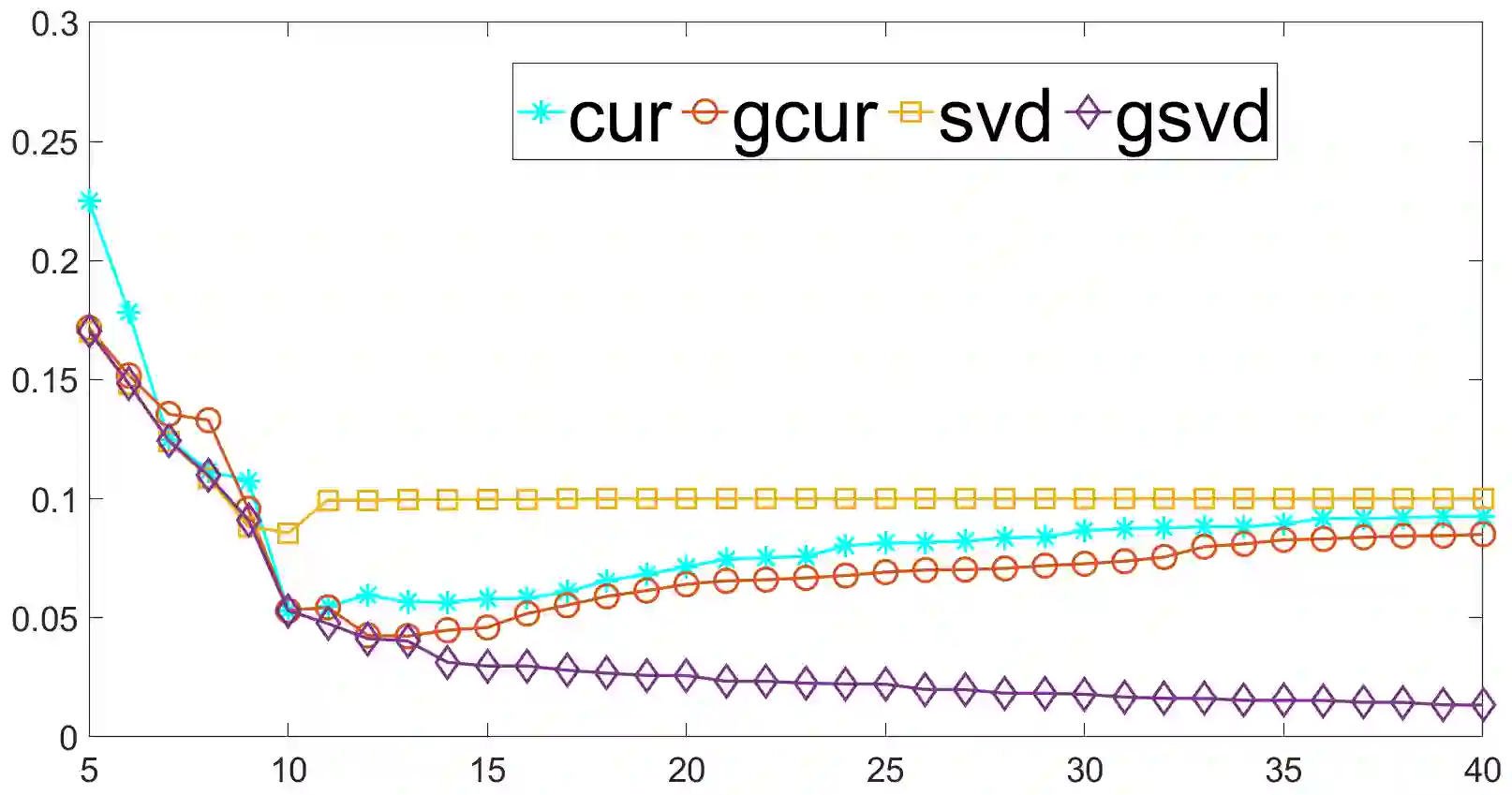
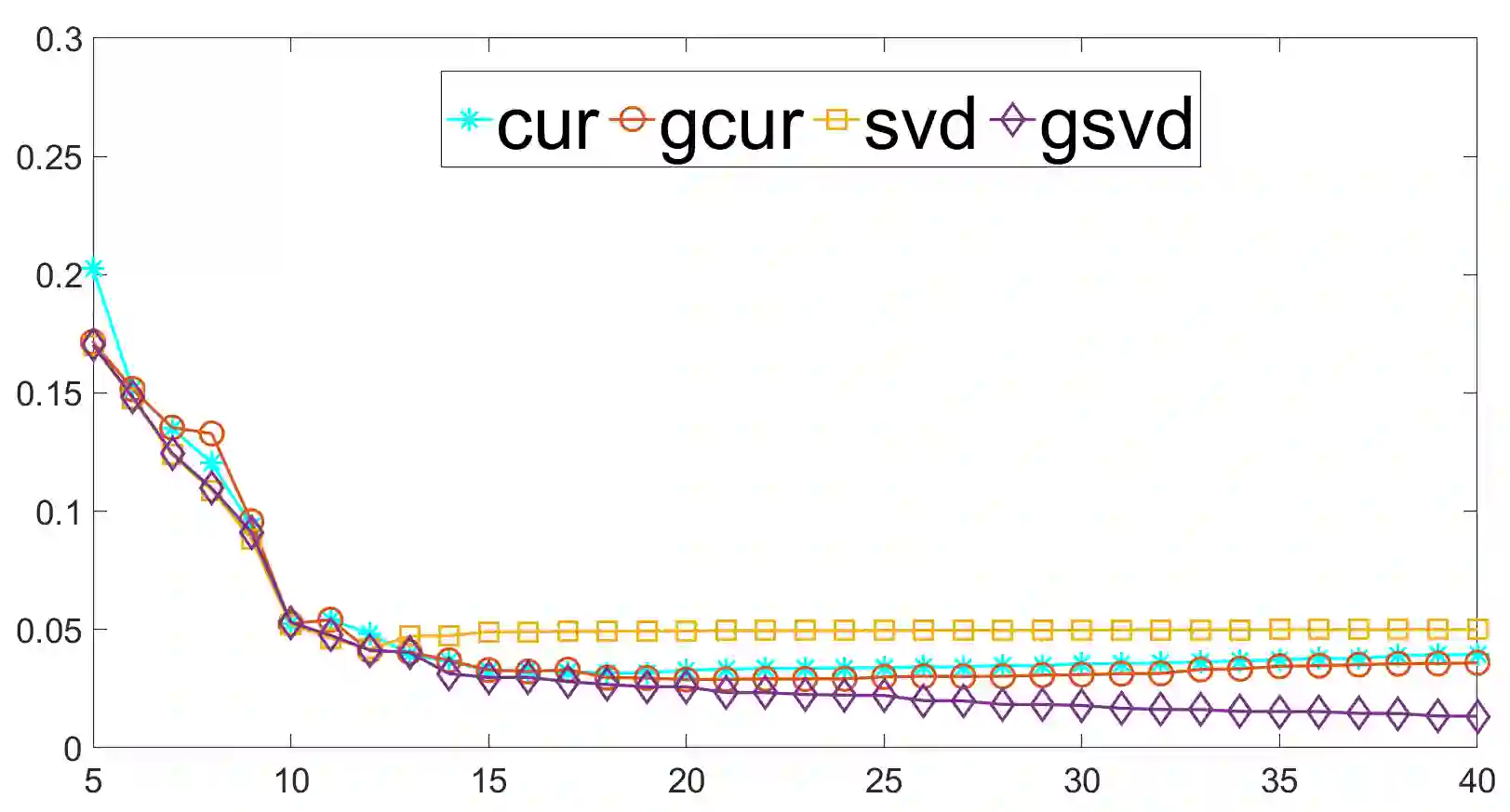
We propose a generalized CUR (GCUR) decomposition for matrix pairs $(A, B)$. Given matrices $A$ and $B$ with the same number of columns, such a decomposition provides low-rank approximations of both matrices simultaneously, in terms of some of their rows and columns. We obtain the indices for selecting the subset of rows and columns of the original matrices using the discrete empirical interpolation method (DEIM) on the generalized singular vectors. When $B$ is square and nonsingular, there are close connections between the GCUR of $(A, B)$ and the DEIM-induced CUR of $AB^{-1}$. When $B$ is the identity, the GCUR decomposition of $A$ coincides with the DEIM-induced CUR decomposition of $A$. We also show a similar connection between the GCUR of $(A, B)$ and the CUR of $AB^+$ for a nonsquare but full-rank matrix $B$, where $B^+$ denotes the Moore--Penrose pseudoinverse of $B$. While a CUR decomposition acts on one data set, a GCUR factorization jointly decomposes two data sets. The algorithm may be suitable for applications where one is interested in extracting the most discriminative features from one data set relative to another data set. In numerical experiments, we demonstrate the advantages of the new method over the standard CUR approximation; for recovering data perturbed with colored noise and subgroup discovery.
翻译:我们建议采用通用单向矢量的通用CUR(GCUR)分解法(美元、B美元),如果基质(A、B)和美元(B美元)与列数相同,则这种分解同时提供两个基质的低位近似值,按其部分行数和列数计算,我们获得使用离散经验内插法(DEIM)在通用单向矢量上选择一组行和列数的指数。当B美元为平方和非正值时,GCUR(A、B)美元与DEIM(CUR)引起的CUR(美元-美元-美元-美元)之间有着密切的连接。当美元为特性时,GUR(美元)分解密与最初的CUR(美元)分解法(美元)的分解法(美元)相吻合。在不平面但不平面但全价的基数(B美元)中,美元表示摩尔-PER(美元)分解法(美元)的相对直径直径法(美元)的利差(美元)值为CUR(CUR)值)的精确值(美元)的精确值(美元)的利差(美元)的利(美元)值(美元)值(美元)值(美元)值(美元)值(美元)值),同时表示一种正值(美元)数据(美元)比值(CUR)比值(美元)数据)比值(CUR)比值(美元)比值(美元)比值(美元)比值(美元)比值(美元)比值(美元)比值)数据(美元)比值(美元)比值(美元)比值(美元)比值(美元)比值(美元)比值(美元)比值(美元)与另一种数据(美元)比值(美元)比值(美元)比值(美元)比值(美元)比值(美元)数据(CUR)比值(美元)比值)比值(美元)比值(美元)比值(美元)比值(美元)比值)比值(美元)比值(美元)的基)的基)数据)的基)数据(美元)的基值(CUR)数据(美元)的另一种)。