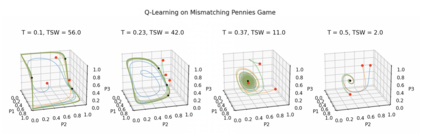
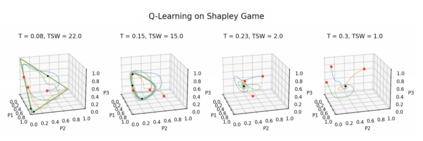
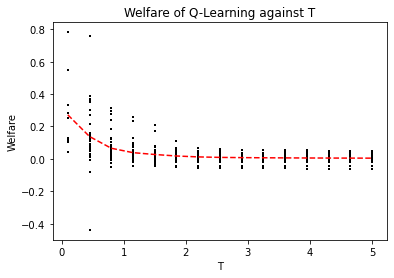
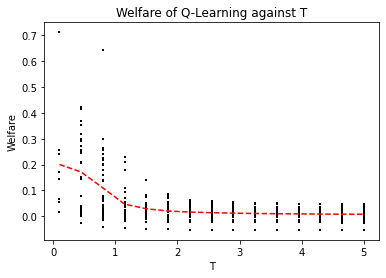
Achieving convergence of multiple learning agents in general $N$-player games is imperative for the development of safe and reliable machine learning (ML) algorithms and their application to autonomous systems. Yet it is known that, outside the bounds of simple two-player games, convergence cannot be taken for granted. To make progress in resolving this problem, we study the dynamics of smooth Q-Learning, a popular reinforcement learning algorithm which quantifies the tendency for learning agents to explore their state space or exploit their payoffs. We show a sufficient condition on the rate of exploration such that the Q-Learning dynamics is guaranteed to converge to a unique equilibrium in any game. We connect this result to games for which Q-Learning is known to converge with arbitrary exploration rates, including weighted Potential games and weighted zero sum polymatrix games. Finally, we examine the performance of the Q-Learning dynamic as measured by the Time Averaged Social Welfare, and comparing this with the Social Welfare achieved by the equilibrium. We provide a sufficient condition whereby the Q-Learning dynamic will outperform the equilibrium even if the dynamics do not converge.
翻译:为了发展安全可靠的机器学习算法并将其应用到自主系统中,一般而言,实现多种学习代理人的趋同是必不可少的。然而,众所周知,在简单的双玩游戏之外,不能将趋同视为理所当然。为了在解决这一问题方面取得进展,我们研究顺利的Q-学习动态,这是一种大众强化学习算法,它量化了学习代理人探索其国家空间或利用其报酬的倾向。我们显示了探索速度的足够条件,保证了Q-学习动态在任何游戏中趋于独特的平衡。我们把这一结果与已知Q-学习与任意勘探率趋同的游戏联系起来,包括加权潜在游戏和加权零和多米特克游戏。最后,我们审查按时间平均社会福利衡量的Q-学习动态的性能,并将它与平衡所实现的社会福利进行比较。我们提供了充分的条件,使Q-学习动态即使动态没有趋同,也会超过平衡。