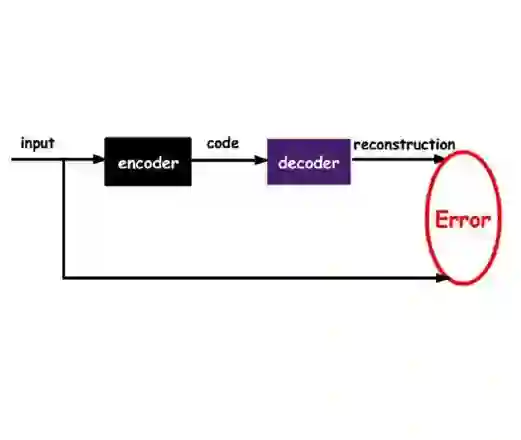
In analyzing and assessing the condition of dynamical systems, it is necessary to account for nonlinearity. Recent advances in computation have rendered previously computationally infeasible analyses readily executable on common computer hardware. However, in certain use cases, such as uncertainty quantification or high precision real-time simulation, the computational cost remains a challenge. This necessitates the adoption of reduced-order modelling methods, which can reduce the computational toll of such nonlinear analyses. In this work, we propose a reduction scheme relying on the exploitation of an autoencoder as means to infer a latent space from output-only response data. This latent space, which in essence approximates the system's nonlinear normal modes (NNMs), serves as an invertible reduction basis for the nonlinear system. The proposed machine learning framework is then complemented via the use of long short term memory (LSTM) networks in the reduced space. These are used for creating an nonlinear reduced-order model (ROM) of the system, able to recreate the full system's dynamic response under a known driving input.
翻译:在分析和评估动态系统的状况时,有必要考虑到非线性。最近的计算进展使得以前在共同计算机硬件上进行不可行的计算分析变得不易执行。然而,在某些使用的情况下,如不确定性量化或高精度实时模拟,计算成本仍然是一项挑战。这需要采用减少顺序建模方法,这样可以减少非线性分析的计算成本。在这项工作中,我们建议采用一个减少计划,利用自动编码器作为从仅输出响应数据中推断潜在空间的手段。这种潜在空间实质上接近了系统的非线性正常模式(NNMS),是非线性系统不可逆的削减基础。随后,拟议的机器学习框架通过在缩小的空间使用长期短期内存网络加以补充。这些功能用于创建系统非线性减序模型(ROM),能够在已知的驱动输入下重新建立整个系统的动态反应。