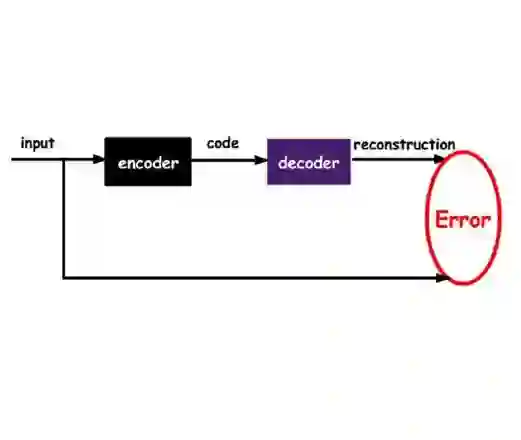
Understanding the latent spaces learned by deep learning models is crucial in exploring how they represent and generate complex data. Autoencoders (AEs) have played a key role in the area of representation learning, with numerous regularization techniques and training principles developed not only to enhance their ability to learn compact and robust representations, but also to reveal how different architectures influence the structure and smoothness of the lower-dimensional non-linear manifold. We strive to characterize the structure of the latent spaces learned by different autoencoders including convolutional autoencoders (CAEs), denoising autoencoders (DAEs), and variational autoencoders (VAEs) and how they change with the perturbations in the input. By characterizing the matrix manifolds corresponding to the latent spaces, we provide an explanation for the well-known observation that the latent spaces of CAE and DAE form non-smooth manifolds, while that of VAE forms a smooth manifold. We also map the points of the matrix manifold to a Hilbert space using distance preserving transforms and provide an alternate view in terms of the subspaces generated in the Hilbert space as a function of the distortion in the input. The results show that the latent manifolds of CAE and DAE are stratified with each stratum being a smooth product manifold, while the manifold of VAE is a smooth product manifold of two symmetric positive definite matrices and a symmetric positive semi-definite matrix.
翻译:暂无翻译