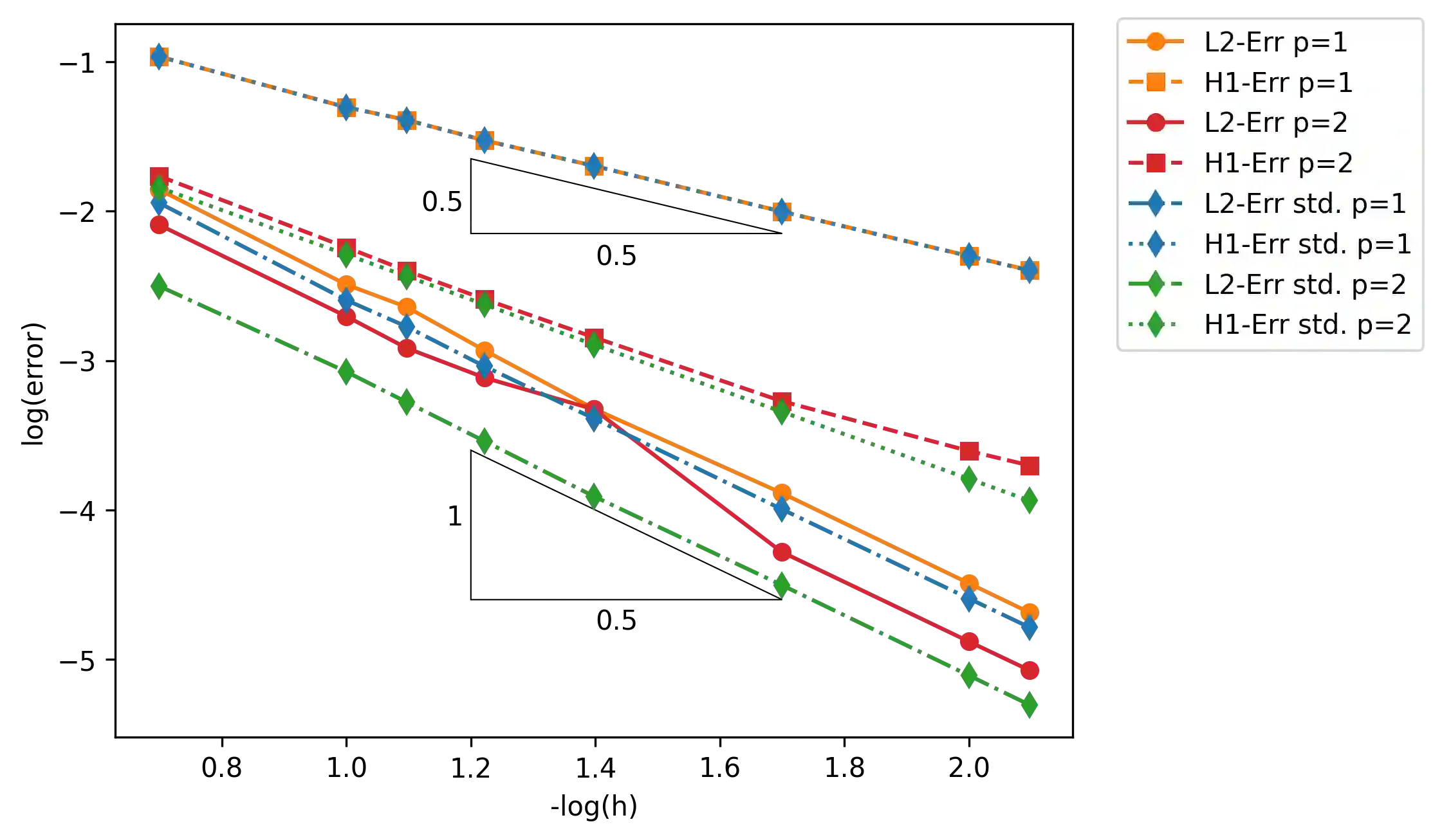
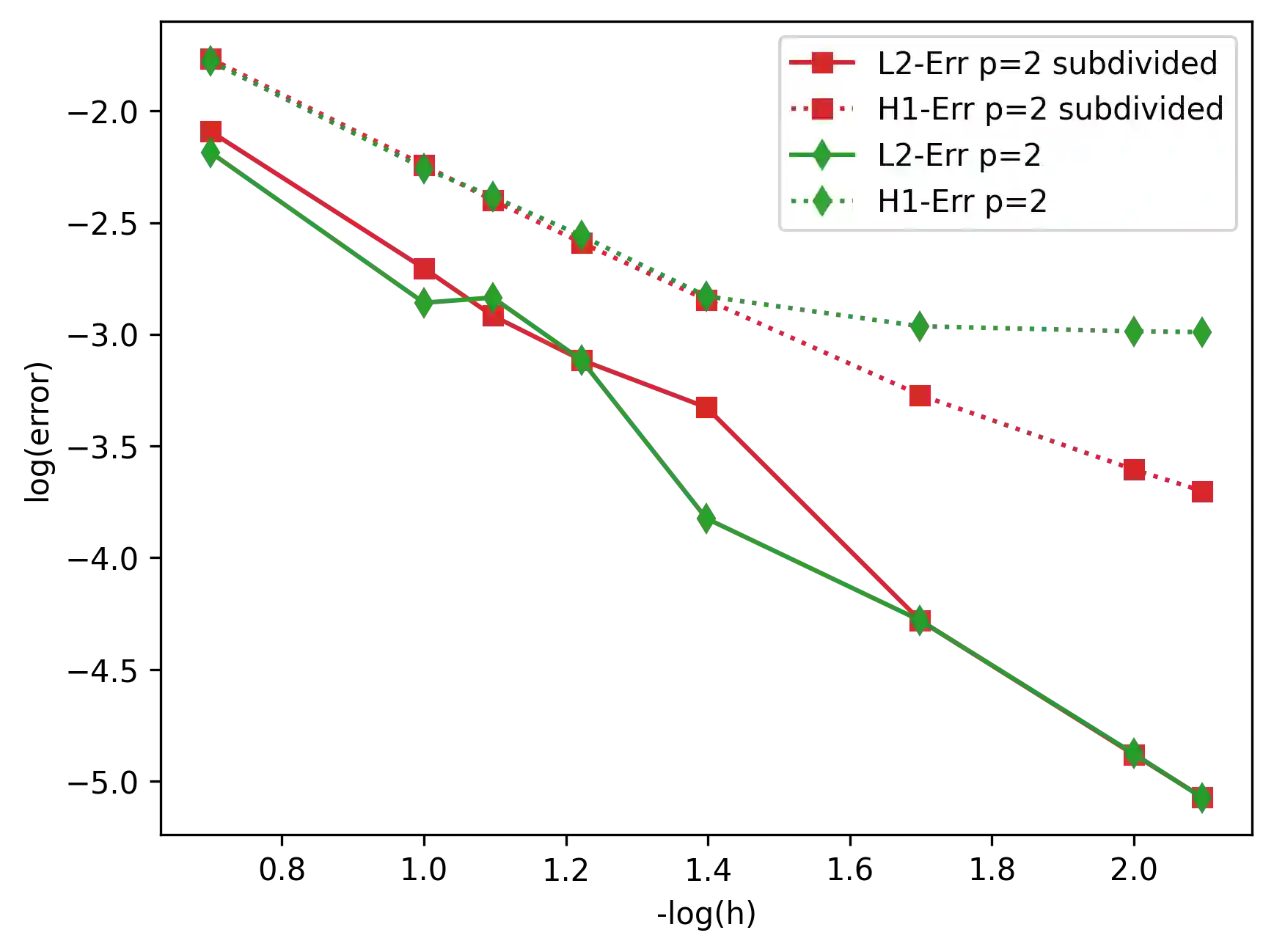
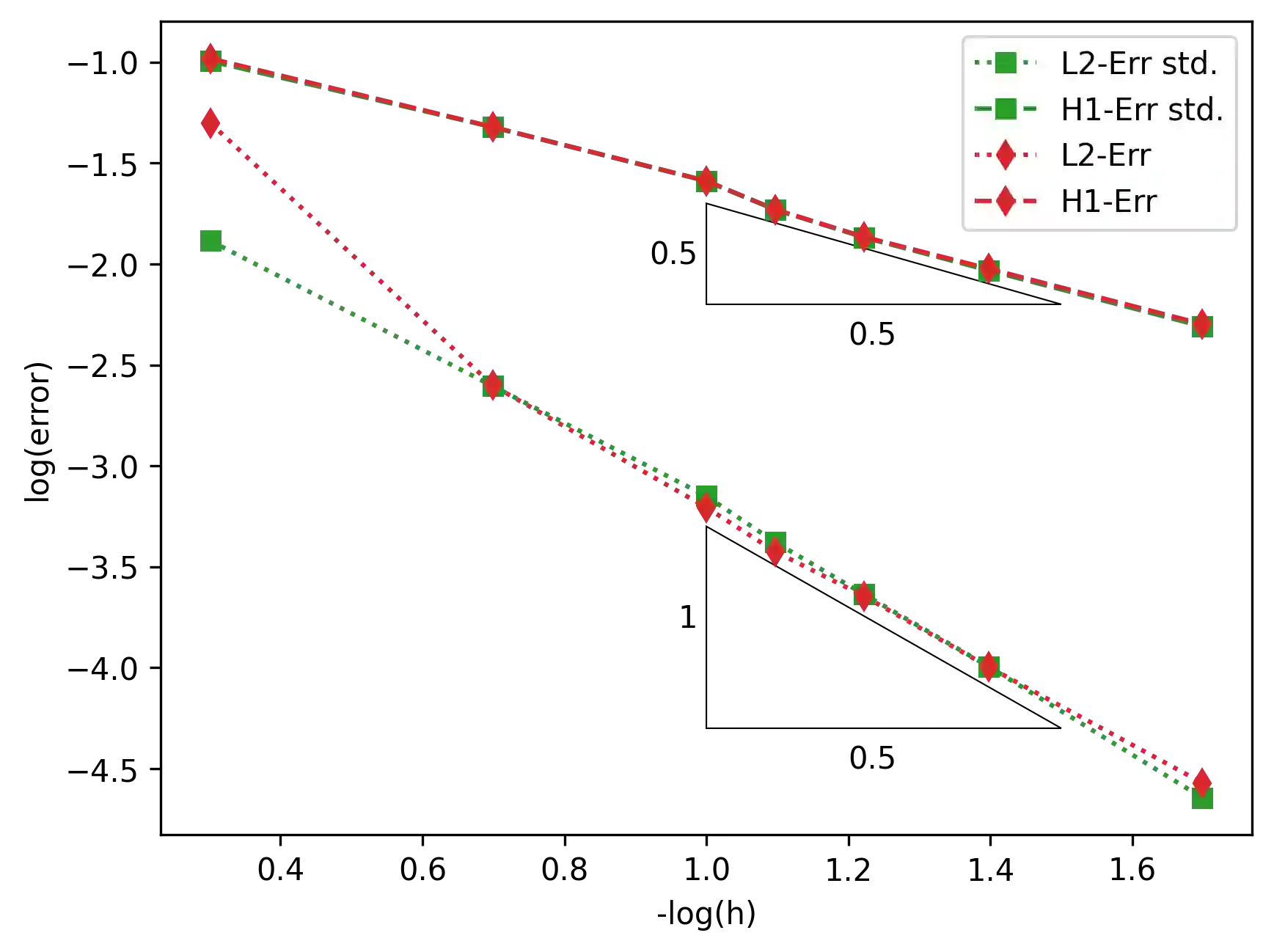
We consider time-harmonic scalar transmission problems between dielectric and dispersive materials with generalized Lorentz frequency laws. For certain frequency ranges such equations involve a sign-change in their principle part. Due to the resulting loss of coercivity properties, the numerical simulation of such problems is demanding. Furthermore, the related eigenvalue problems are nonlinear and give rise to additional challenges. We present a new finite element method for both of these types of problems, which is based on a weakly coercive reformulation of the PDE. The new scheme can handle $C^{1,1}$-interfaces consisting piecewise of elementary geometries. Neglecting quadrature errors, the method allows for a straightforward convergence analysis. In our implementation we apply a simple, but nonstandard quadrature rule to achieve negligible quadrature errors. We present computational experiments in 2D and 3D for both source and eigenvalue problems which confirm the stability and convergence of the new scheme.
翻译:暂无翻译