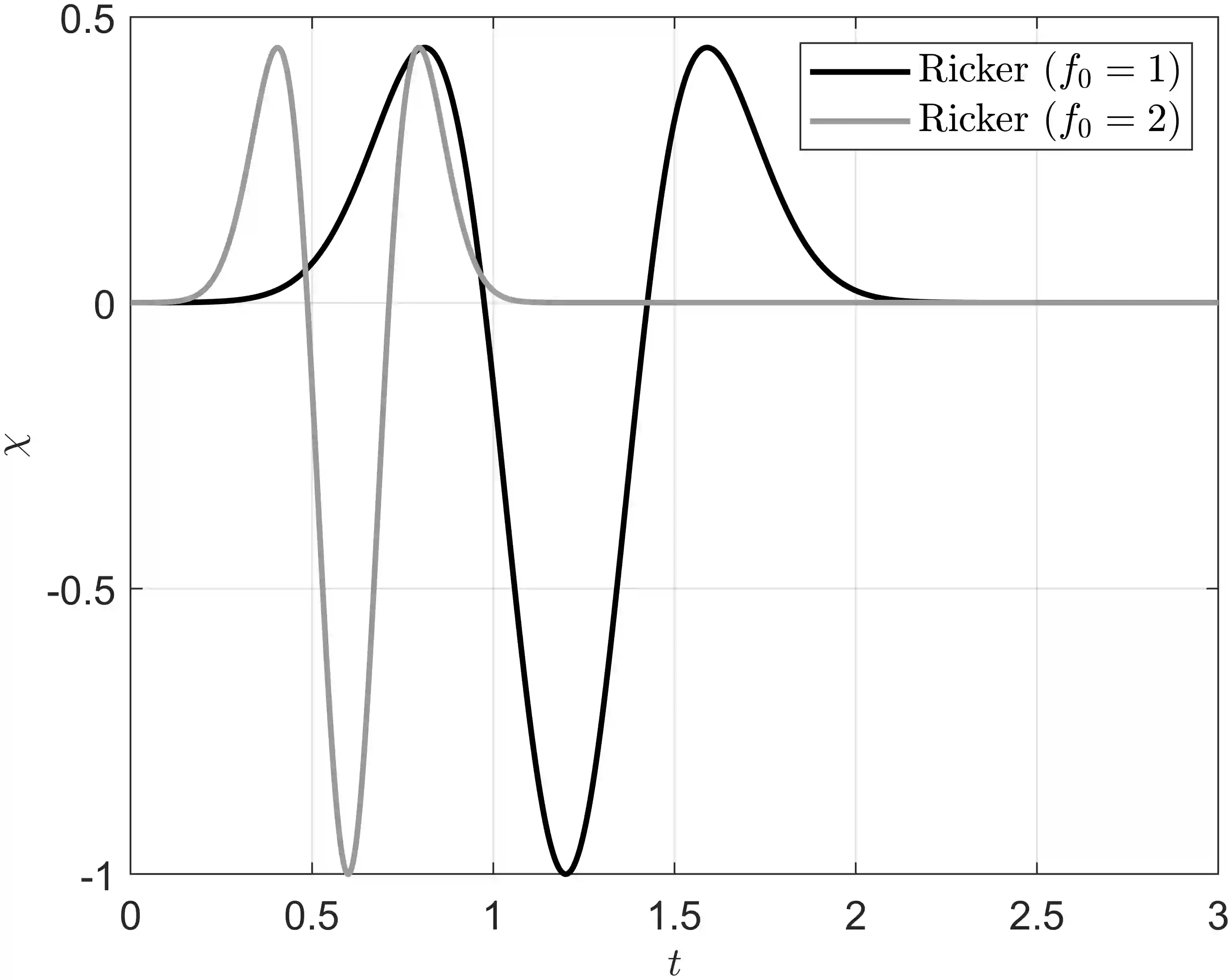
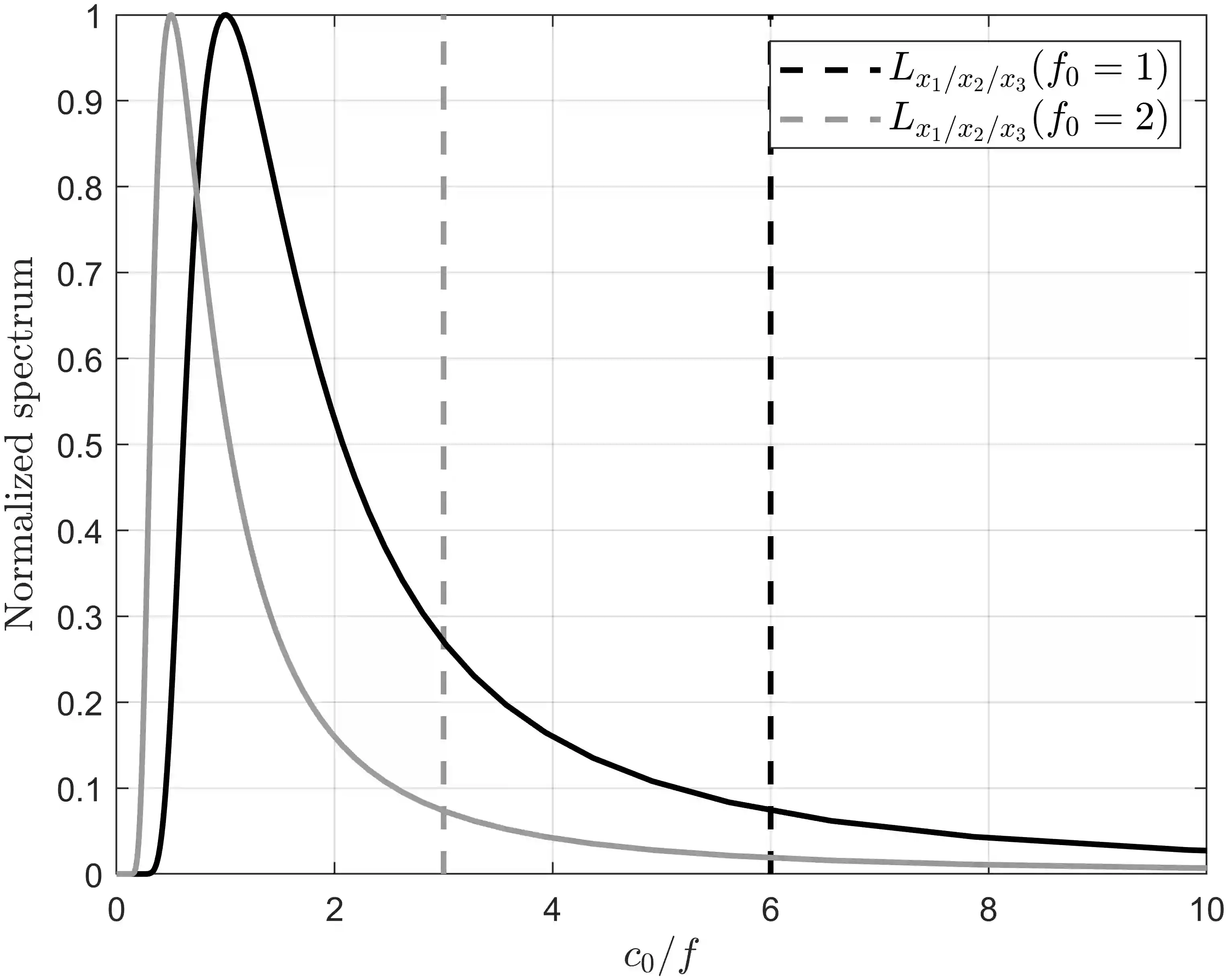
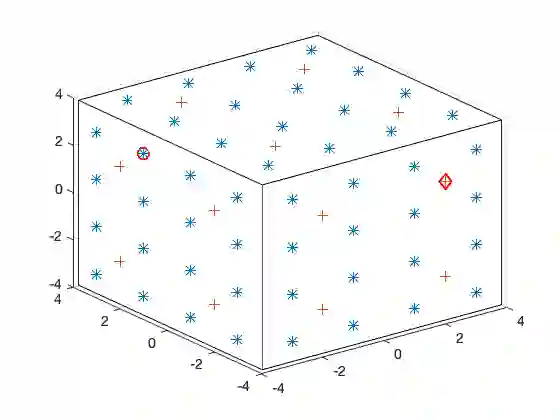
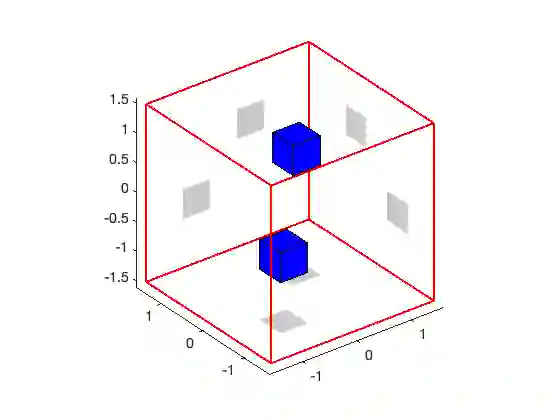
The Time Domain Linear Sampling Method for Determining the Shape of a Scatterer using Electromagnetic Waves

The time domain linear sampling method (TD-LSM) solves inverse scattering problems using time domain data by creating an indicator function for the support of the unknown scatterer. It involves only solving a linear integral equation called the near-field equation using different data from sampling points that probe the domain where the scatterer is located. To date, the method has been used for the acoustic wave equation and has been tested for several different types of scatterers, i.e. sound hard, impedance, and penetrable, and for wave-guides. In this paper, we extend the TD-LSM to the time dependent Maxwell's system with impedance boundary conditions - a similar analysis handles the case of a perfectly electrically conducting (PEC) body. We provide an analysis that supports the use of the TD-LSM for this problem, and preliminary numerical tests of the algorithm. Our analysis relies on the Laplace transform approach previously used for the acoustic wave equation. This is the first application of the TD-LSM in electromagnetism.