Scalable Sensitivity and Uncertainty Analysis for Causal-Effect Estimates of Continuous-Valued Interventions

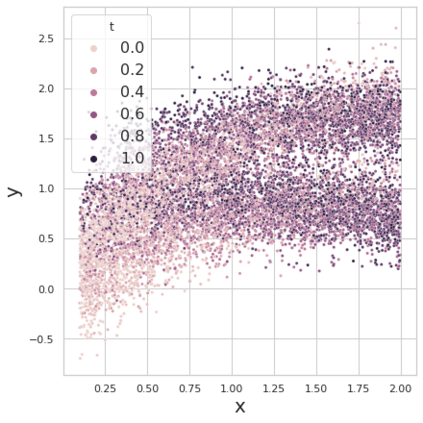
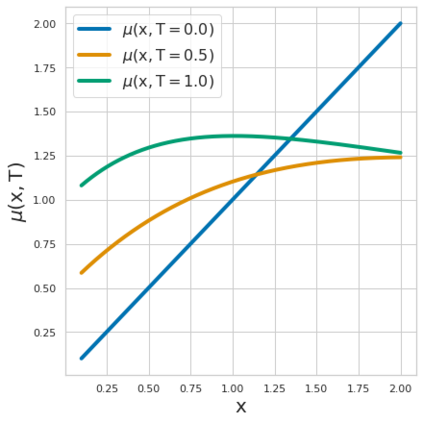
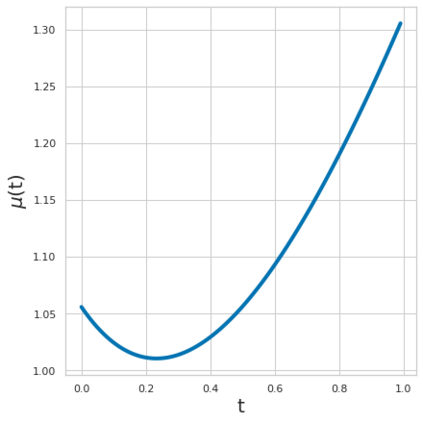
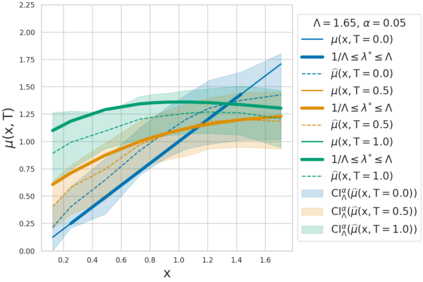
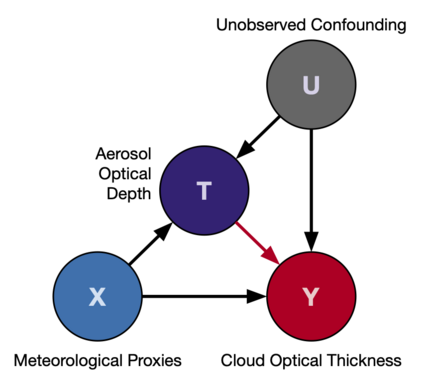
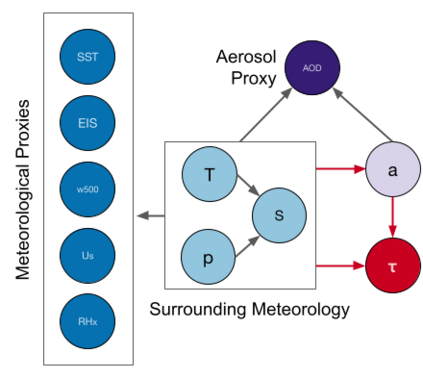
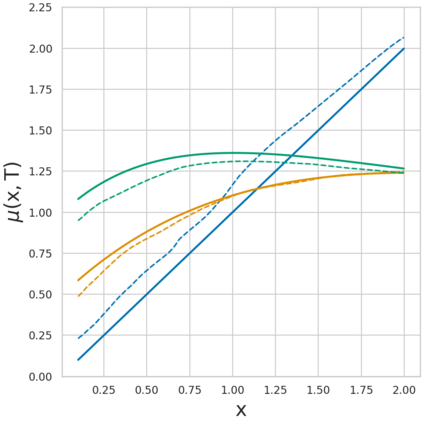
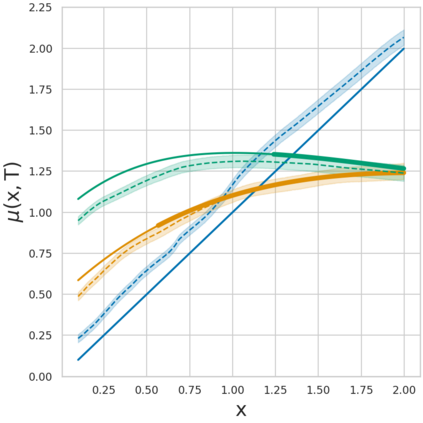
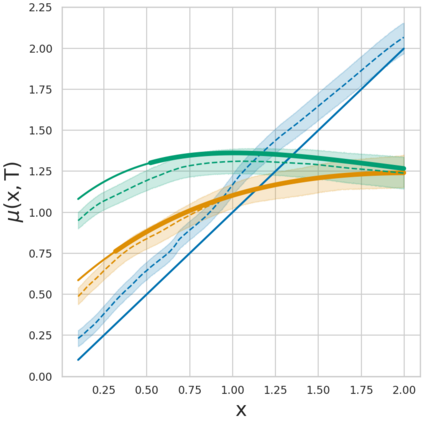
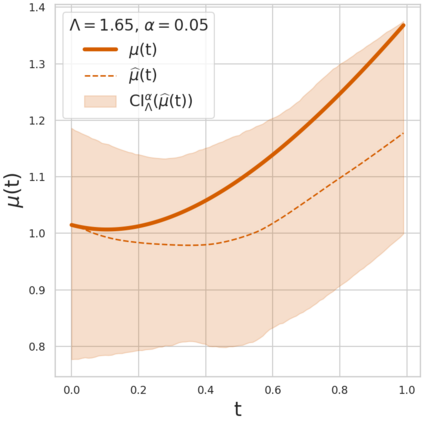
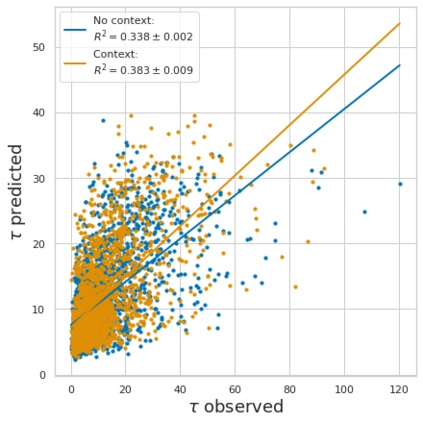
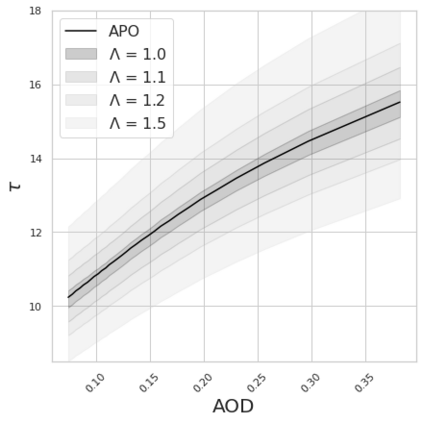
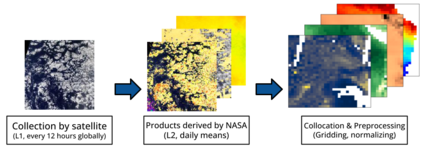
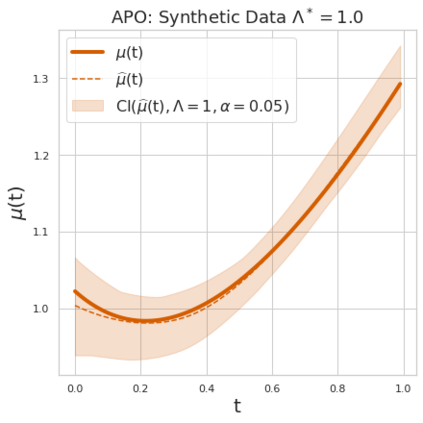
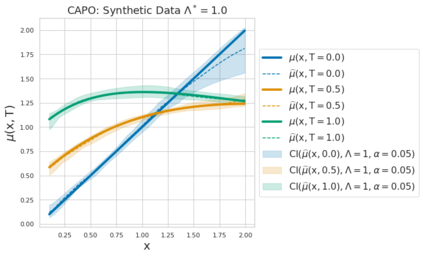
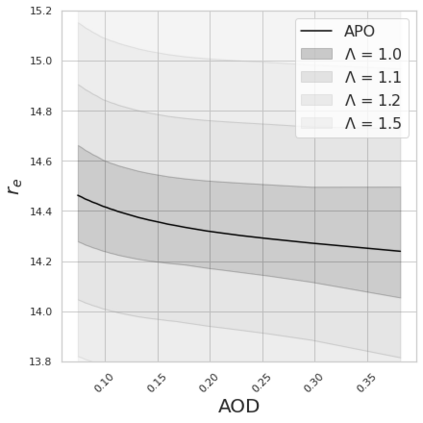
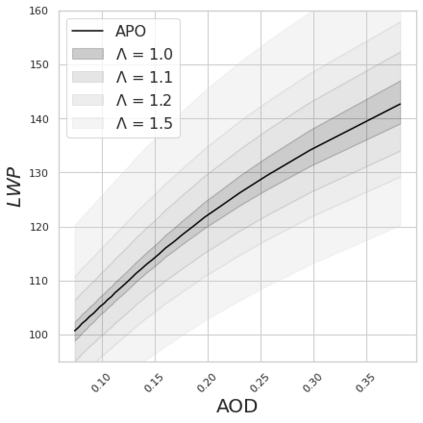
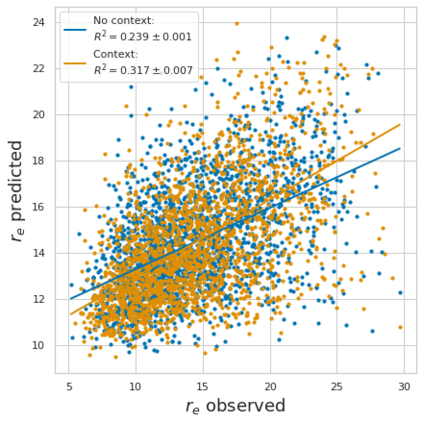
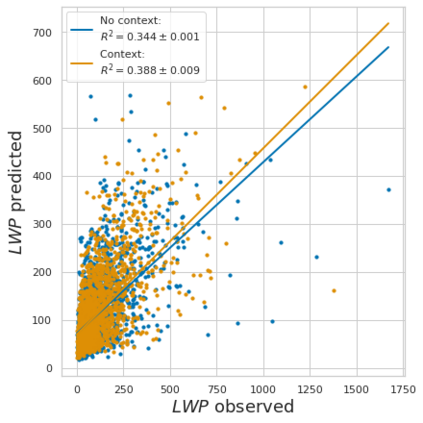
Estimating the effects of continuous-valued interventions from observational data is critically important in fields such as climate science, healthcare, and economics. Recent work focuses on designing neural-network architectures and regularization functions to allow for scalable estimation of average and individual-level dose response curves from high-dimensional, large-sample data. Such methodologies assume ignorability (all confounding variables are observed) and positivity (all levels of treatment can be observed for every unit described by a given covariate value), which are especially challenged in the continuous treatment regime. Developing scalable sensitivity and uncertainty analyses that allow us to understand the ignorance induced in our estimates when these assumptions are relaxed receives less attention. Here, we develop a continuous treatment-effect marginal sensitivity model (CMSM) and derive bounds that agree with both the observed data and a researcher-defined level of hidden confounding. We introduce a scalable algorithm to derive the bounds and uncertainty-aware deep models to efficiently estimate these bounds for high-dimensional, large-sample observational data. We validate our methods using both synthetic and real-world experiments. For the latter, we work in concert with climate scientists interested in evaluating the climatological impacts of human emissions on cloud properties using satellite observations from the past 15 years: a finite-data problem known to be complicated by the presence of a multitude of unobserved confounders.