Lossy compression of statistical data using quantum annealer

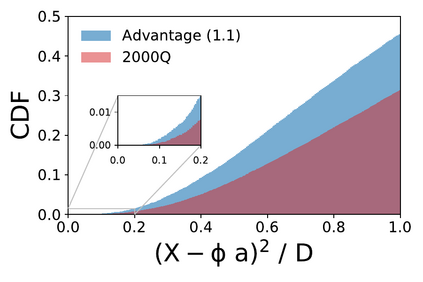
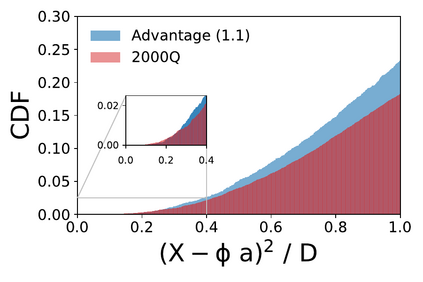
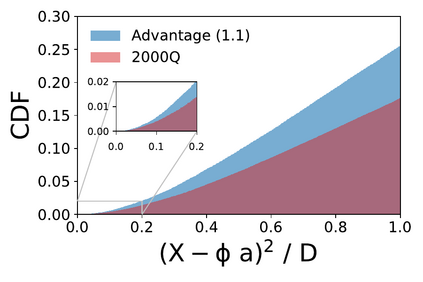
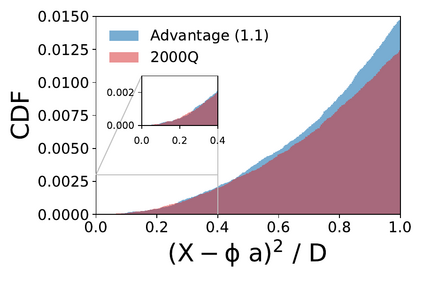
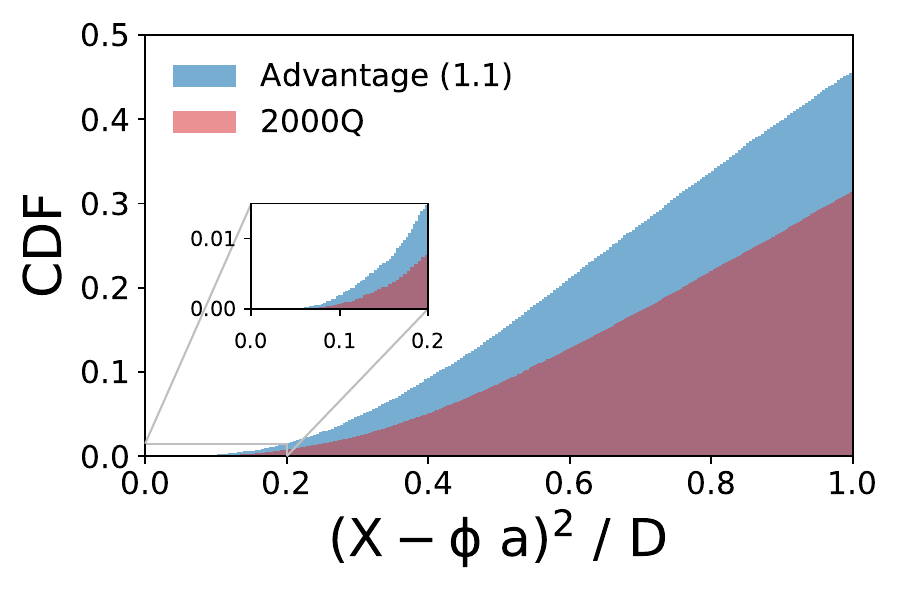
We present a new lossy compression algorithm for statistical floating-point data through a representation learning with binary variables. The algorithm finds a set of basis vectors and their binary coefficients that precisely reconstruct the original data. The optimization for the basis vectors is performed classically, while binary coefficients are retrieved through both simulated and quantum annealing for comparison. A bias correction procedure is also presented to estimate and eliminate the error and bias introduced from the inexact reconstruction of the lossy compression for statistical data analyses. The compression algorithm is demonstrated on two different datasets of lattice quantum chromodynamics simulations. The results obtained using simulated annealing show 3.5 times better compression performance than the algorithms based on a neural-network autoencoder and principal component analysis. Calculations using quantum annealing also show promising results, but performance is limited by the integrated control error of the quantum processing unit, which yields large uncertainties in the biases and coupling parameters. Hardware comparison is further studied between the previous generation D-Wave 2000Q and the current D-Wave Advantage system. Our study shows that the Advantage system is more likely to obtain low-energy solutions for the problems than the 2000Q.