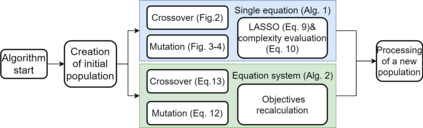
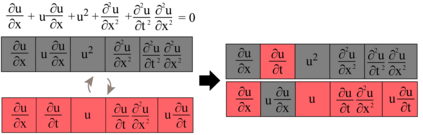
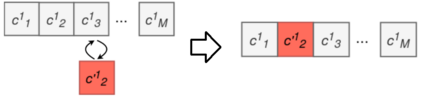
Usually, the systems of partial differential equations (PDEs) are discovered from observational data in the single vector equation form. However, this approach restricts the application to the real cases, where, for example, the form of the external forcing is of interest. In the paper, a multi-objective co-evolution algorithm is described. The single equations within the system and the system itself are evolved simultaneously to obtain the system. This approach allows discovering the systems with the form-independent equations. In contrast to the single vector equation, a component-wise system is more suitable for expert interpretation and, therefore, for applications. The example of the two-dimensional Navier-Stokes equation is considered.
翻译:通常,部分差异方程式(PDEs)系统是从单一矢量方程式的观测数据中发现的,但这一方法将应用限制在实际情况下,例如外部强迫的形式值得注意。在本文中,描述了多目标的共演算法。系统内部的单一方程式和系统本身是同时演进的,以获得系统。这一方法允许用单向量方程式发现系统。与单一矢量方程式不同,一个构件-方法更适合专家解释,因此也更适合应用。二维纳维尔-斯托克斯方程式的例子也得到了考虑。