Multiagent Transition Systems with Faults: Protocol-Stack Mathematics for Distributed Computing

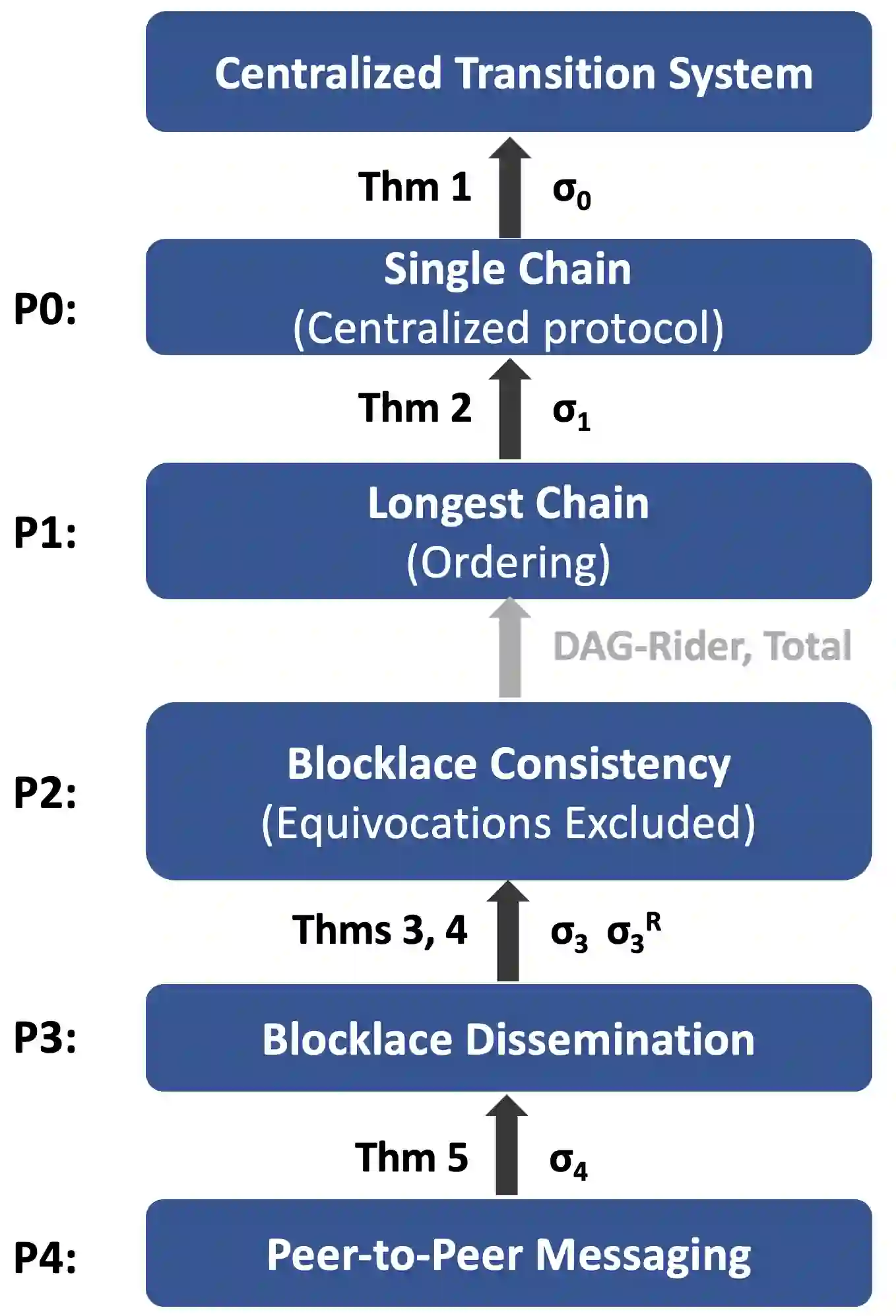
Presently, the practice of distributed computing is such that problems exist in a mathematical realm different from their solutions: a problem is presented as a set of requirements on possible process or system behaviors, and its solution is presented as algorithmic pseudocode satisfying the requirements. Here, we present a novel mathematical realm, termed \emph{multiagent transition systems with faults}, that aims to accommodate both distributed computing problems and their solutions. A problem is presented as a specification -- a multiagent transition system -- and a solution as an implementation of the specification by another, lower-level multiagent transition system, which may be proven to be resilient to a given set of faults. This duality of roles of a multiagent transition system can be exploited all the way from a high-level distributed computing problem description down to an agreed-upon base layer, say TCP/IP, resulting in a mathematical protocol stack where each protocol in the stack both implements the protocol above it and serves as a specification for the protocol below it. Correct implementations are compositional and thus provide also an implementation of the protocol stack as a whole. The framework also offers a formal -- yet natural and expressive -- notions of faults, fault-resilient implementations, and their composition.