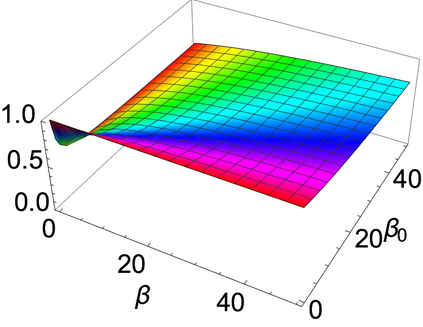
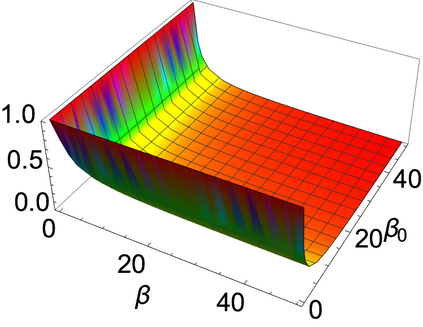
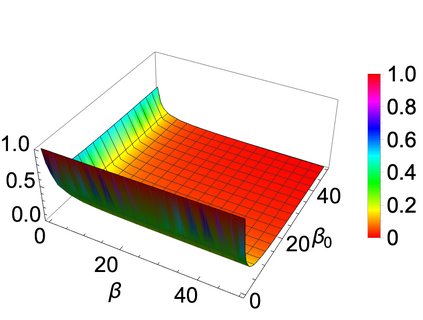
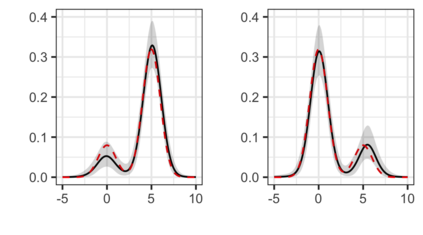
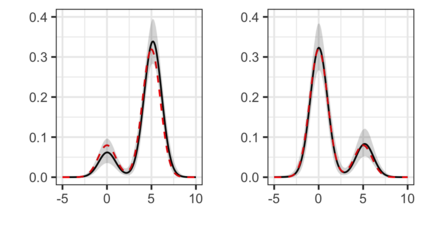
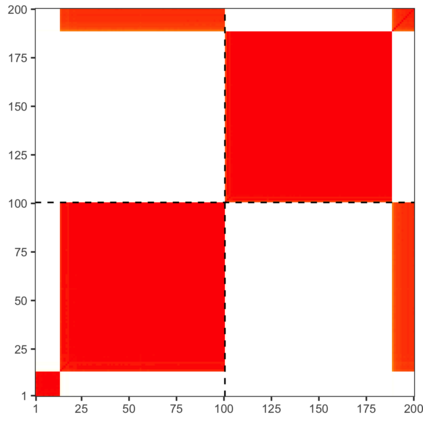
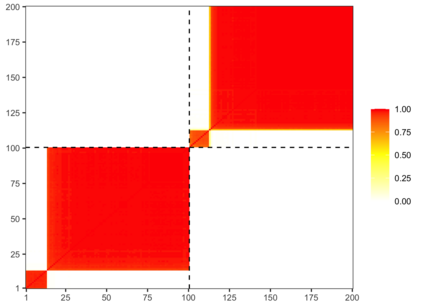
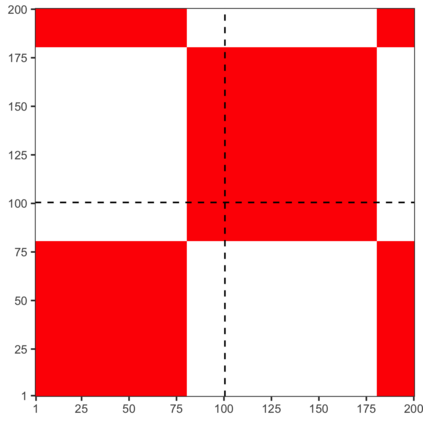
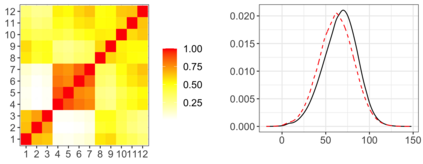
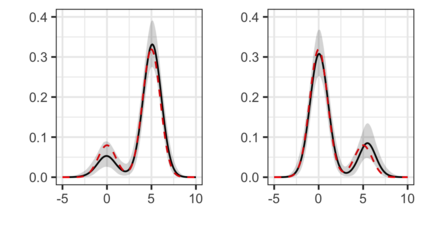
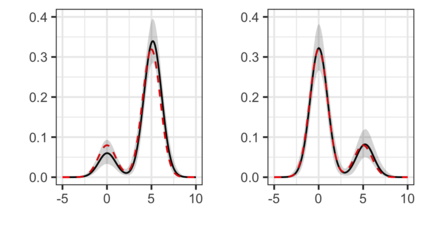
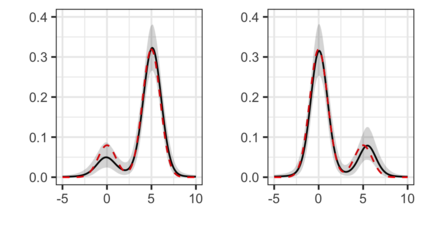
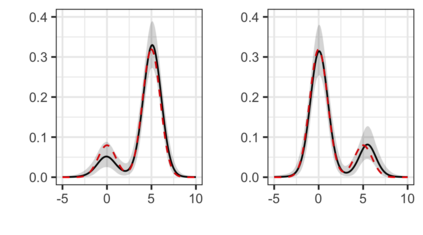
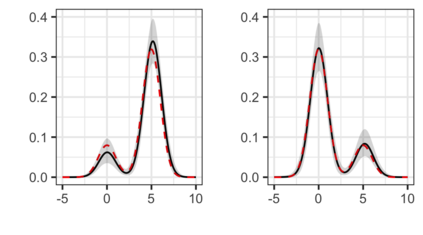
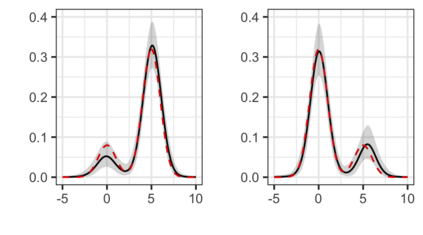
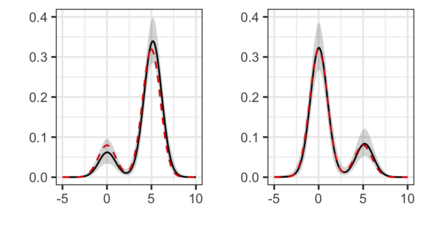
The Bayesian approach to inference stands out for naturally allowing borrowing information across heterogeneous populations, with different samples possibly sharing the same distribution. A popular Bayesian nonparametric model for clustering probability distributions is the nested Dirichlet process, which however has the drawback of grouping distributions in a single cluster when ties are observed across samples. With the goal of achieving a flexible and effective clustering method for both samples and observations, we investigate a nonparametric prior that arises as the composition of two different discrete random structures and derive a closed-form expression for the induced distribution of the random partition, the fundamental tool regulating the clustering behavior of the model. On the one hand, this allows to gain a deeper insight into the theoretical properties of the model and, on the other hand, it yields an MCMC algorithm for evaluating Bayesian inferences of interest. Moreover, we single out limitations of this algorithm when working with more than two populations and, consequently, devise an alternative more efficient sampling scheme, which as a by-product, allows testing homogeneity between different populations. Finally, we perform a comparison with the nested Dirichlet process and provide illustrative examples of both synthetic and real data.
翻译:贝叶斯推论法表明自然允许不同人群之间借款,不同样本可能共享相同的分布。一个受欢迎的巴伊西亚非参数模型组群概率分布模式是嵌套式的狄里赫莱工艺,但当观察到不同样本之间的关联时,该模型组群分布会有一个缺陷。此外,为了对样本和观测结果采用灵活有效的群集方法,我们先研究一种非参数方法,它产生于两种不同的离散随机结构的构成,并产生一种封闭式的表达方式,用于随机分区的随机分布,这是调节模型群集行为的基本工具。一方面,这可以更深入地了解模型的理论特性,另一方面,它产生一种MCMC算法,用于评价贝伊斯人的引力。此外,我们指出在与两个以上人群合作时,这种算法的局限性,因此,我们设计一种效率更高的采样方法,作为副产品,可以测试不同人群之间的同质性。最后,我们与嵌巢式的狄里赫莱工艺进行了比较,并提供合成和合成数据的示例。