Self-supervised learning for a nonlinear inverse problem with forward operator involving an unknown function arising in Photoacoustic Tomography

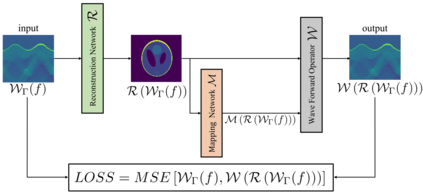
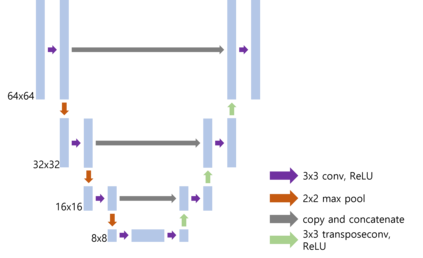
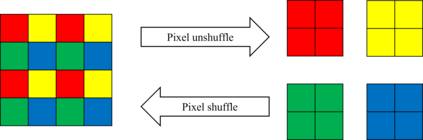
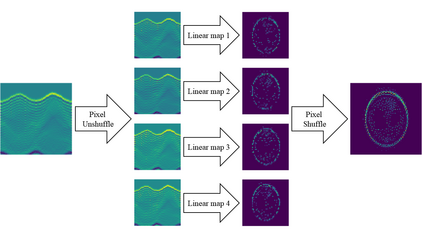
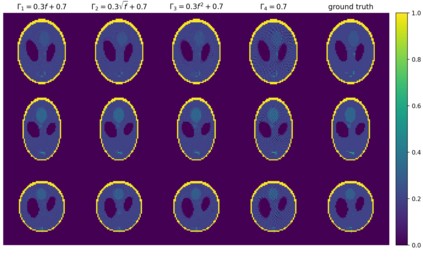
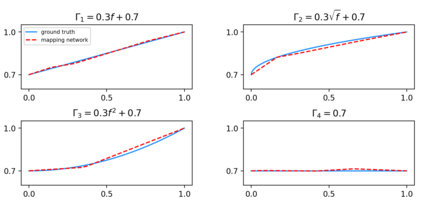
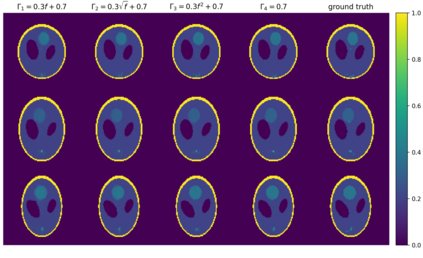
In this article, we concern with a nonlinear inverse problem with forward operator involving an unknown function. The problem arises in diverse applications and is challenging by the presence of the unknown function, which makes it ill-posed. Additionally, the nonlinear nature of the problem makes it difficult to use traditional methods and thus the study has addressed a simplified version of the problem by either linearizing it or assuming knowledge of the unknown function. Here, we propose a self-supervised learning to directly tackle a nonlinear inverse problem involving an unknown function. In particular, we focus on an inverse problem derived in Photoacoustic Tomograpy (PAT) which is a hybrid medical imaging with high resolution and contrast. PAT can be modelled based on the wave equation. The measured data is the solution of the equation restricted to the surface and the initial pressure of the equation contains the biological information on the object of interest. The speed of sound wave in the equation is unknown. Our goal is to determine the initial pressure and the speed of sound wave simultaneously. Under a simple assumption that the sound speed is a function of the initial pressure, the problem becomes a nonlinear inverse problem involving an unknown function. The experimental results demonstrate that the proposed algorithm performs successfully.