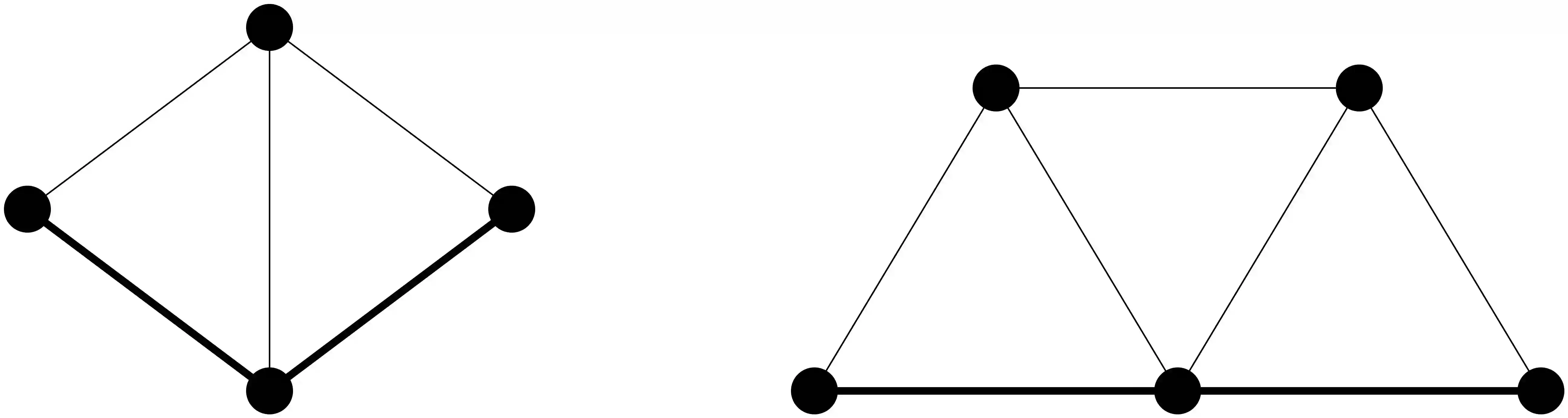
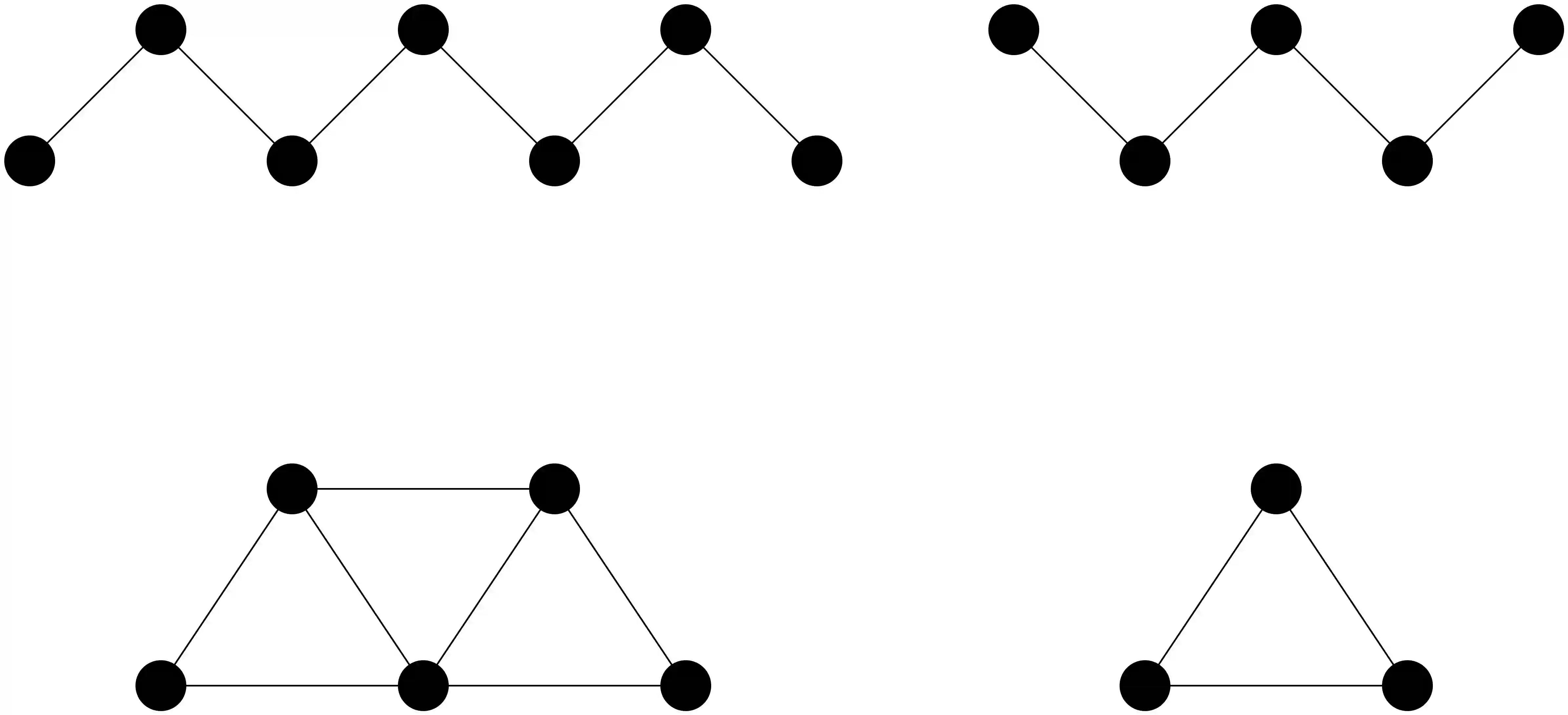
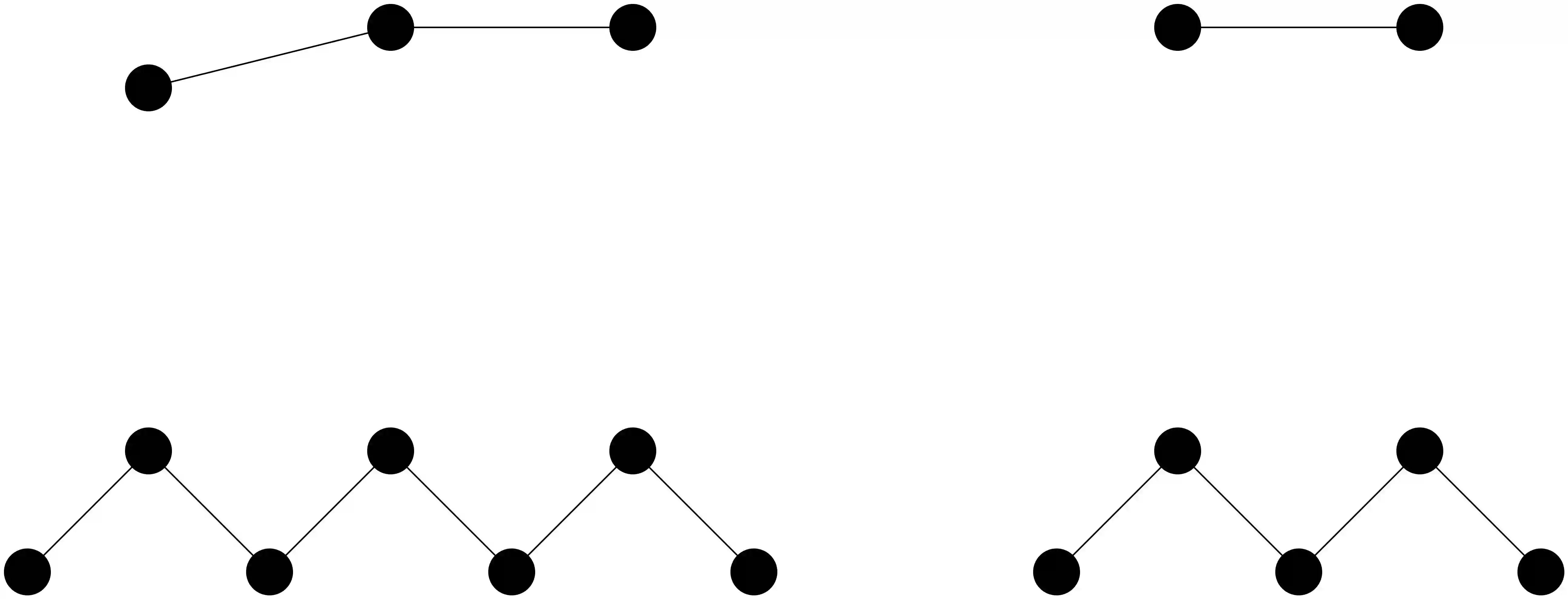
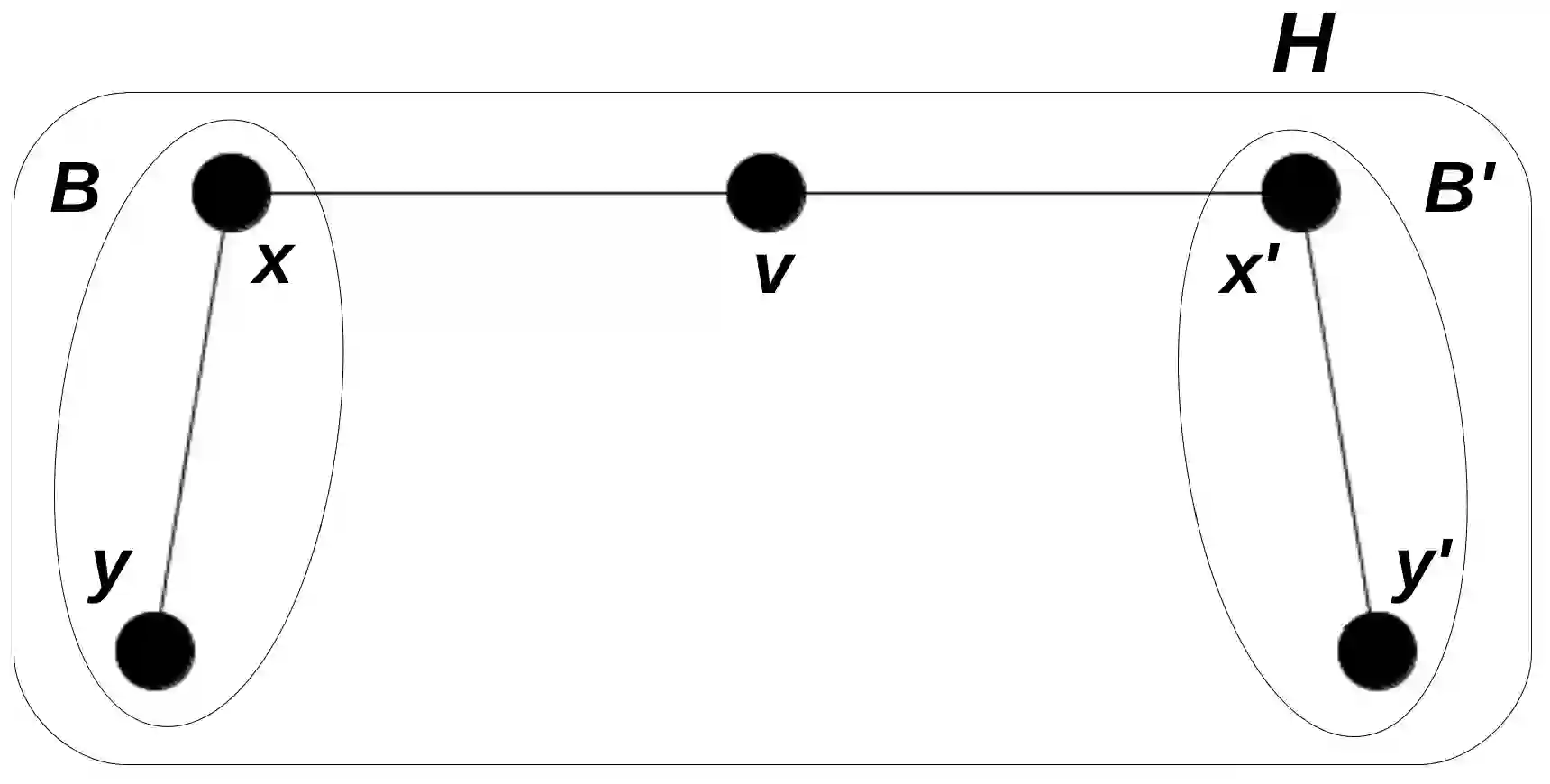
A \textit{biclique} is a maximal bipartite complete induced subgraph of $G$. The \textit{biclique graph} of a graph $G$, denoted by $KB(G)$, is the intersection graph of the family of all bicliques of $G$. In this work we study some structural properties of bicliques graphs which are necessary conditions for a graph to be a biclique graph. In particular, we prove that for biclique graphs that are neither a $K_3$ nor a \textit{diamond}, the number of vertices of degree two is less than half of its vertices. Also, we present forbidden structures. For that, we introduce a natural definition of the distance between bicliques in a graph. We give a formula that relates the distance between bicliques in a graph $G$ and the distance between their respective vertices in $KB(G)$. Using these results, we can prove not only this new necessary condition involving the degree, but also that some graphs are not biclique graphs. For example, we show that the \textit{crown} is the smallest graph that is not a biclique graph although the known necessary condition for biclique graphs holds, answering an open problem about biclique graphs. Finally, we present some interesting related conjectures and open problems.
翻译:\ textit{ biclique} 是一个最大双部分完整的 $G$ 引导子图。 由 $KB (G) 表示的 $G$ 图形 的\ textit{ biclique 图形} 是所有 bicliques $G$ 的家族的交叉图 。 在这项工作中, 我们研究了 bicliques 图形的一些结构属性, 这对于图形成为 biclique 图形是必要的条件。 特别是, 我们证明, 对于既不是 K_ 3 $ 或\ textit{ diamon} 的双曲线图来说, 水平 2 的顶点数量小于其顶点的一半 。 另外, 我们展示了被禁止的结构 。 为此, 我们在图表中引入了一种自然定义 。 我们给出了一个公式, 将 bicliqueque $G$G$ (G) 和 各自的顶点之间的距离联系起来 $KB (G) 。 。 使用这些结果, 我们不仅可以证明这个涉及 度的新的必要条件条件,, 也显示 listrue dealtiquestal 的图形是 riquestal 。