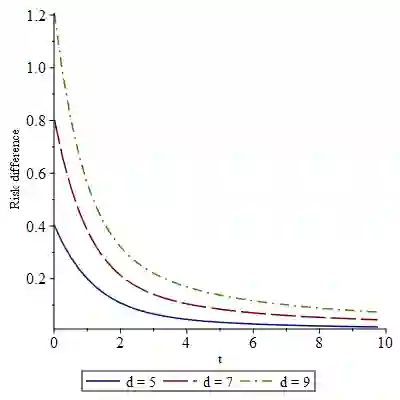
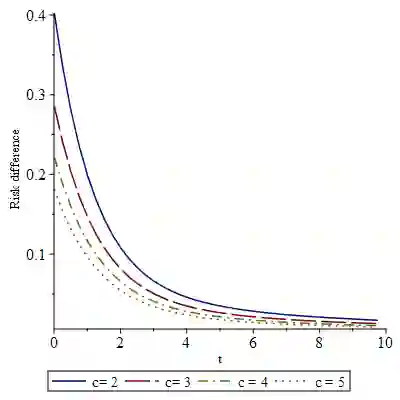
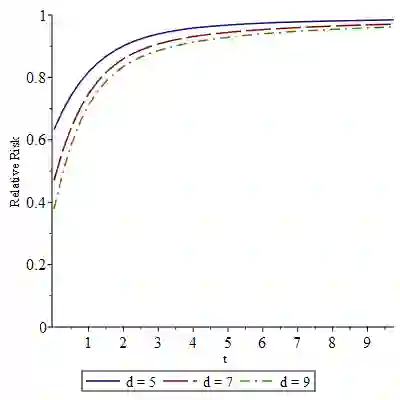
We study frequentist risk properties of predictive density estimators for mean mixtures of multivariate normal distributions, involving an unknown location parameter $\theta \in \mathbb{R}^d$, and which include multivariate skew normal distributions. We provide explicit representations for Bayesian posterior and predictive densities, including the benchmark minimum risk equivariant (MRE) density, which is minimax and generalized Bayes with respect to an improper uniform density for $\theta$. For four dimensions or more, we obtain Bayesian densities that improve uniformly on the MRE density under Kullback-Leibler loss. We also provide plug-in type improvements, investigate implications for certain type of parametric restrictions on $\theta$, and illustrate and comment the findings based on numerical evaluations.
翻译:我们研究多变量正常分布平均混合物的预测密度估计值常年风险特性,其中涉及未知位置参数$\theta\ in\mathbb{R ⁇ d$,其中包括多变量扭曲正常分布,我们为巴伊西亚后方和预测密度提供了明确的表述,包括基准最小风险等差密度(MRE)密度(MRE),该等值密度与美元不适当统一密度相比是微型和泛海湾。对于四个或更多维,我们获得了巴伊西亚密度,这些密度在Kullback-Leiberl损失条件下的MRE密度一致提高。我们还提供插式改进,调查某类对$\theta$的参数限制的影响,并根据数字评估来说明和评论调查结果。