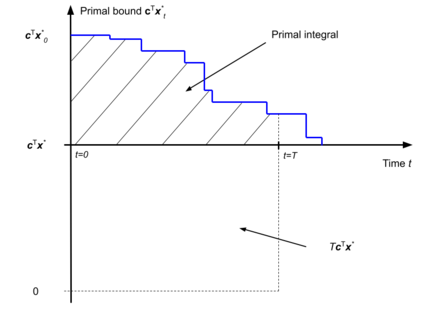
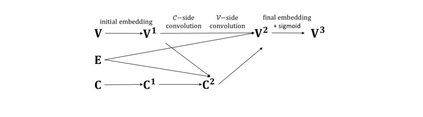
Finding a better feasible solution in a shorter time is an integral part of solving Mixed Integer Programs. We present a post-hoc method based on Neural Diving to build heuristics more flexibly. We hypothesize that variables with higher confidence scores are more definite to be included in the optimal solution. For our hypothesis, we provide empirical evidence that confidence threshold technique produces partial solutions leading to final solutions with better primal objective values. Our method won 2nd place in the primal task on the NeurIPS 2021 ML4CO competition. Also, our method shows the best score among other learning-based methods in the competition.
翻译:短期内找到更好的可行解决办法是解决混合整数程序的一个组成部分。 我们提出一种基于神经分层的后热方法,以更灵活地建立超自然学。 我们假设信心分高的变量更确定地包含在最佳解决办法中。 对于我们的假设,我们提供了经验证据,证明信任阈值技术产生了部分解决办法,最终的解决办法具有更好的原始客观价值。我们的方法在NeurIPS 2021 ML4CO 竞赛的原始任务中赢得了第2位。此外,我们的方法展示了竞赛中其他学习方法中的最佳分数。