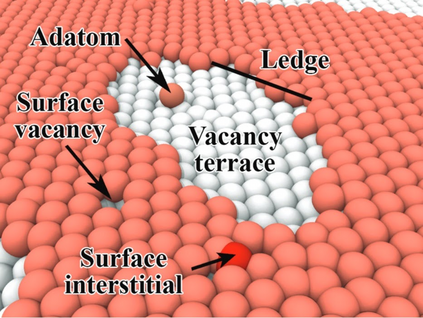
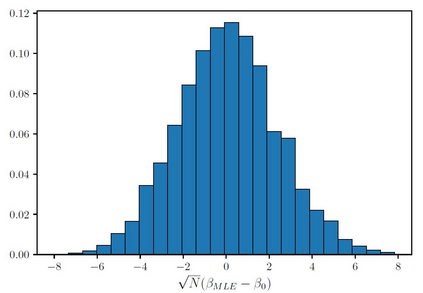
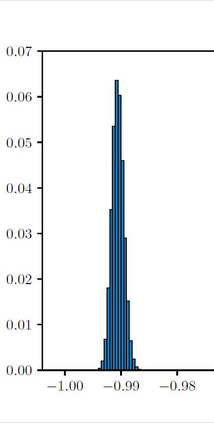
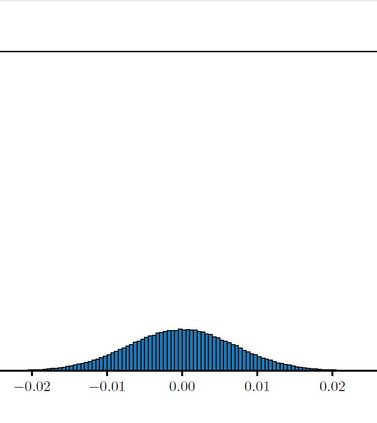
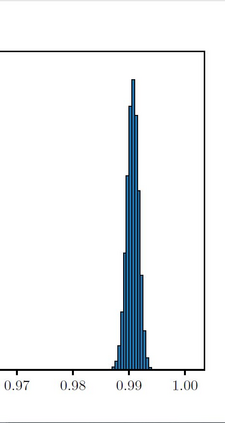
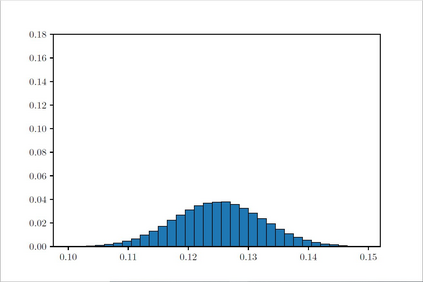
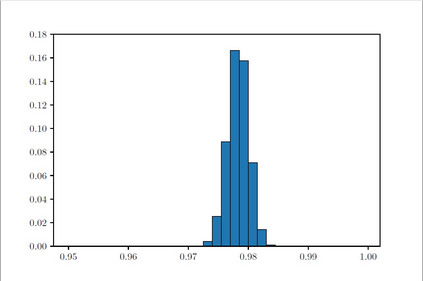
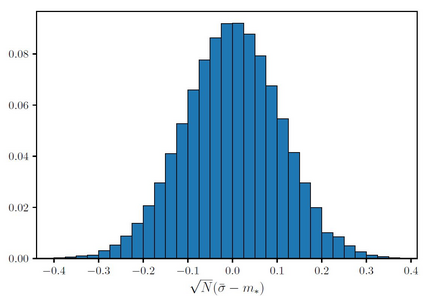
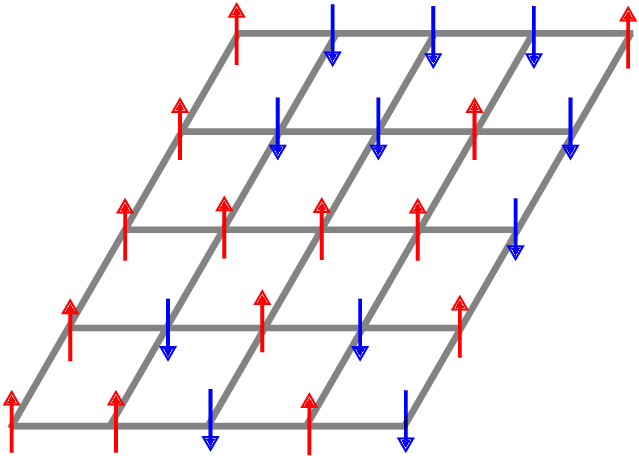
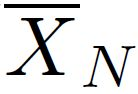The Ising model is a celebrated example of a Markov random field, introduced in statistical physics to model ferromagnetism. This is a discrete exponential family with binary outcomes, where the sufficient statistic involves a quadratic term designed to capture correlations arising from pairwise interactions. However, in many situations the dependencies in a network arise not just from pairs, but from peer-group effects. A convenient mathematical framework for capturing higher-order dependencies, is the $p$-tensor Ising model, where the sufficient statistic consists of a multilinear polynomial of degree $p$. This thesis develops a framework for statistical inference of the natural parameters in $p$-tensor Ising models. We begin with the Curie-Weiss Ising model, where we unearth various non-standard phenomena in the asymptotics of the maximum-likelihood (ML) estimates of the parameters, such as the presence of a critical curve in the interior of the parameter space on which these estimates have a limiting mixture distribution, and a surprising superefficiency phenomenon at the boundary point(s) of this curve. ML estimation fails in more general $p$-tensor Ising models due to the presence of a computationally intractable normalizing constant. To overcome this issue, we use the popular maximum pseudo-likelihood (MPL) method, which avoids computing the inexplicit normalizing constant based on conditional distributions. We derive general conditions under which the MPL estimate is $\sqrt{N}$-consistent, where $N$ is the size of the underlying network. Finally, we consider a more general Ising model, which incorporates high-dimensional covariates at the nodes of the network, that can also be viewed as a logistic regression model with dependent observations. In this model, we show that the parameters can be estimated consistently under sparsity assumptions on the true covariate vector.
翻译:以Ising 模型为标志性 Markov 随机 字段的著名范例。 这是在统计物理中引入的 Markov 随机字段, 用于模拟铁磁学。 这是一个离散的指数式组合, 具有二进制结果, 足够的统计涉及一个四进制的术语, 用来捕捉双向互动产生的关联。 但是, 在许多情形中, 网络的依赖性不仅来自对配对, 也来自对等群体效应。 获取更高排序矢量依赖性的方便数学框架是 $- 向量 模式, 足够的统计包括多线性多线性多级多级多级多级的美元。 这个统计为以 $- 十进制的自然参数的统计推导出一个框架。 我们从Curie- Weissing Ising 模型开始, 各种非标准现象在最大类似值的参数中, 最接近值的模型可以持续地显示我们内部的正变值空间的正值曲线曲线曲线曲线曲线曲线曲线曲线值值值值, 。 在基点上, 最常态的计算中, 最精确的模型可以持续地显示我们总的轨道的轨道的模型可以持续的计算。