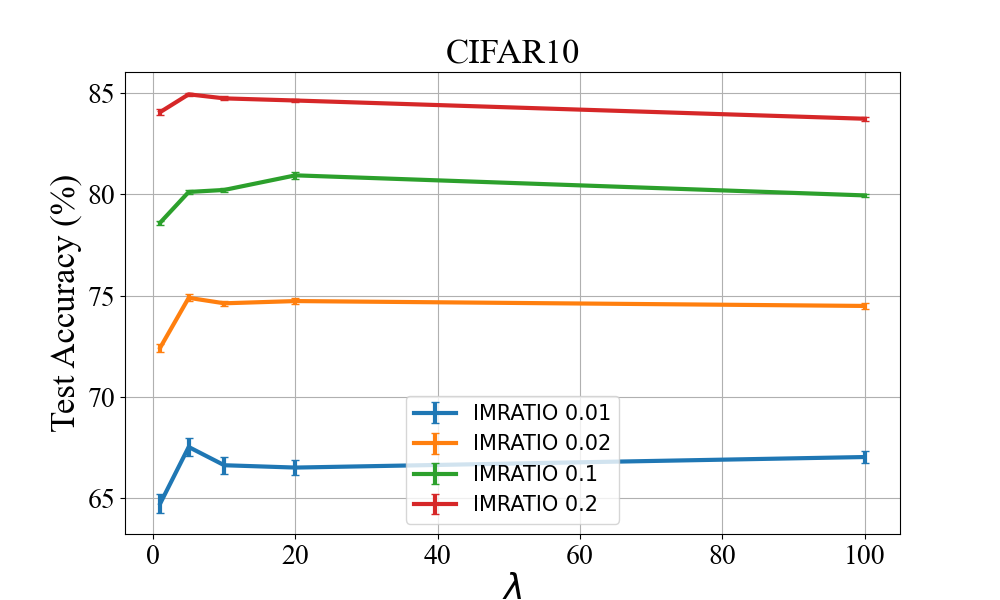
In this paper, we propose a practical online method for solving a class of distributionally robust optimization (DRO) with non-convex objectives, which has important applications in machine learning for improving the robustness of neural networks. In the literature, most methods for solving DRO are based on stochastic primal-dual methods. However, primal-dual methods for DRO suffer from several drawbacks: (1) manipulating a high-dimensional dual variable corresponding to the size of data is time expensive; (2) they are not friendly to online learning where data is coming sequentially. To address these issues, we consider a class of DRO with an KL divergence regularization on the dual variables, transform the min-max problem into a compositional minimization problem, and propose practical duality-free online stochastic methods without requiring a large mini-batch size. We establish the state-of-the-art complexities of the proposed methods with and without a Polyak-\L ojasiewicz (PL) condition of the objective. Empirical studies on large-scale deep learning tasks (i) demonstrate that our method can speed up the training by more than 2 times than baseline methods and save days of training time on a large-scale dataset with $\sim$ 265K images, and (ii) verify the supreme performance of DRO over Empirical Risk Minimization (ERM) on imbalanced datasets. Of independent interest, the proposed method can be also used for solving a family of stochastic compositional problems with state-of-the-art complexities.
翻译:在本文中,我们提出一种实用的在线方法,以解决具有非硬度目标的分布式强力优化(DRO)类别,该类别在机器学习中具有重要的应用性,以提高神经网络的稳健性。在文献中,大多数解决DRO的方法都是基于随机性原始-双向方法。然而,DRO的原始双向方法有几个缺点:(1) 操纵一个与数据大小相对应的高维双重变量是昂贵的;(2) 这些数据不便于在数据顺序上出现的在线学习。为了解决这些问题,我们考虑一个具有KL结构差异的DRO类别,对双重变量进行正规化,将微量最大问题转化为最小化问题,并提出实用的双重性在线互见方法,而不需要大小批量。 我们确定拟议方法的复杂程度,既采用,又不采用Polyak-Lojasielwicz (PL) 条件。为了解决这些问题,我们考虑对大规模深度学习任务进行实证化研究(i),将微量值问题转换成最小值问题,用我们的方法可以加快Sirimal-deal la-deal lax latial-deal lax lax lax lax lax lax lax lax lax a lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax