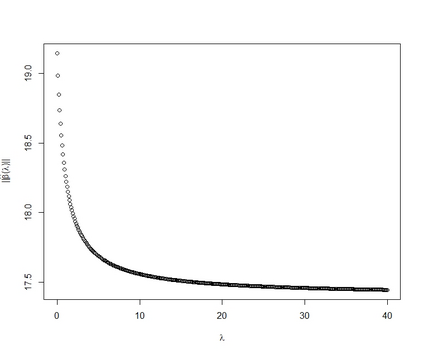
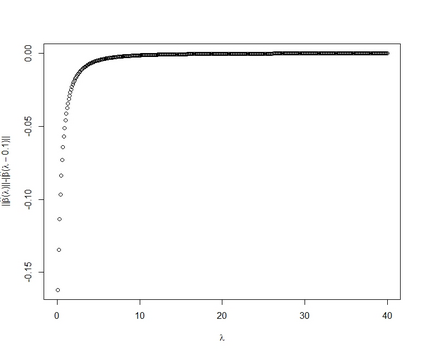
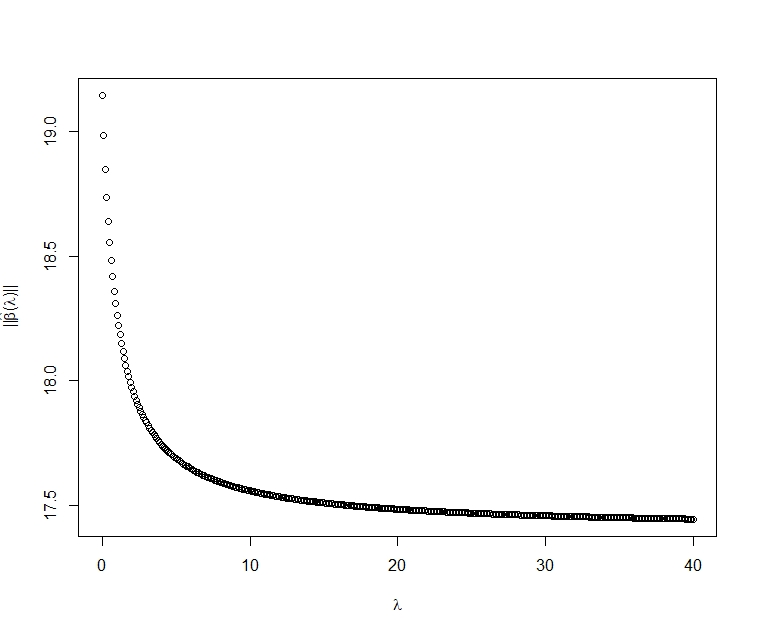
Multicollinearity produces an inflation in the variance of the Ordinary Least Squares estimators due to the correlation between two or more independent variables (including the constant term). A widely applied solution is to estimate with penalized estimators (such as the ridge estimator, the Liu estimator, etc.) which exchange the mean square error by the bias. Although the variance diminishes with these procedures, all seems to indicate that the inference is lost and also the goodness of fit. Alternatively, the raise regression (\cite{Garcia2011} and \cite{Salmeron2017}) allows the mitigation of the problems generated by multicollinearity but without losing the inference and keeping the coefficient of determination. This paper completely formalizes the raise estimator summarizing all the previous contributions: its mean square error, the variance inflation factor, the condition number, the adequate selection of the variable to be raised, the successive raising and the relation between the raise and the ridge estimator. As a novelty, it is also presented the estimation method, the relation between the raise and the residualization, it is analyzed the norm of the estimator and the behaviour of the individual and joint significance test and the behaviour of the mean square error and the coefficient of variation. The usefulness of the raise regression as alternative to mitigate the multicollinearity is illustrated with two empirical applications.
翻译:虽然差异因偏差而缩小,但似乎都表明,由于两个或两个以上独立变量(包括常数)之间的相互关系,普通最低广场估计值的差价产生了通货膨胀。一个广泛应用的解决办法是,用惩罚性估计值(如山脊估测仪、刘测测算仪等)来估算,这些估算值以偏差来交换中方差方差。虽然差异随着这些程序而减少,但所有差异似乎都表明,假设值已经丢失,而且合适性也很好。或者,上升回归值(cite{Garcia2011}和cite{Salmeron2017})使得能够缓解多极性应用产生的问题,但又不失去推论,并保持确定系数。本文完全正式确定了概述以往所有贡献的加比值:其平均平差差、差异性通货膨胀系数、条件号、适当选择要提出变量、不断提高值以及峰值和山脊估估测算仪之间的关系。作为创新方法,还介绍了多极性应用的估算方法、提高值和估算值和估测算值之间的关系,同时分析了其测试性价值和估测算法和估测算法的比值的比值的比值的比值。