Geometric Model Checking of Continuous Space

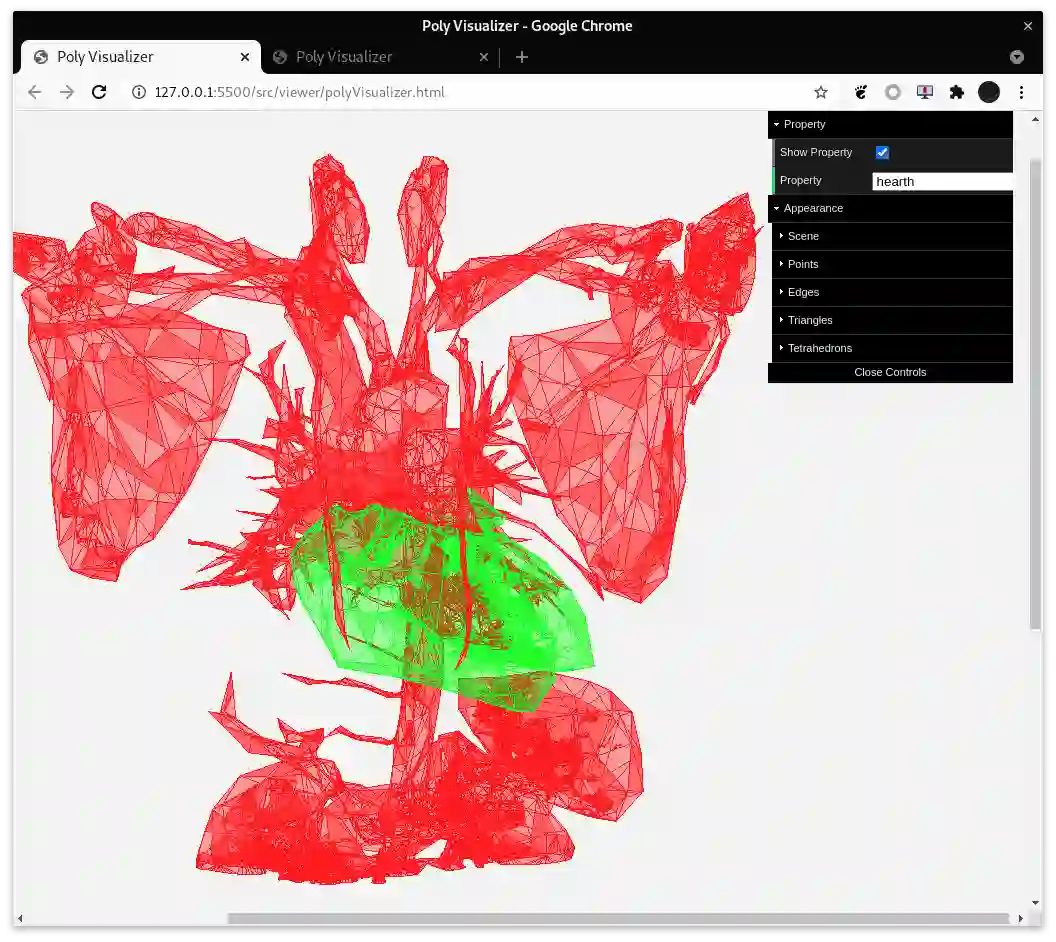
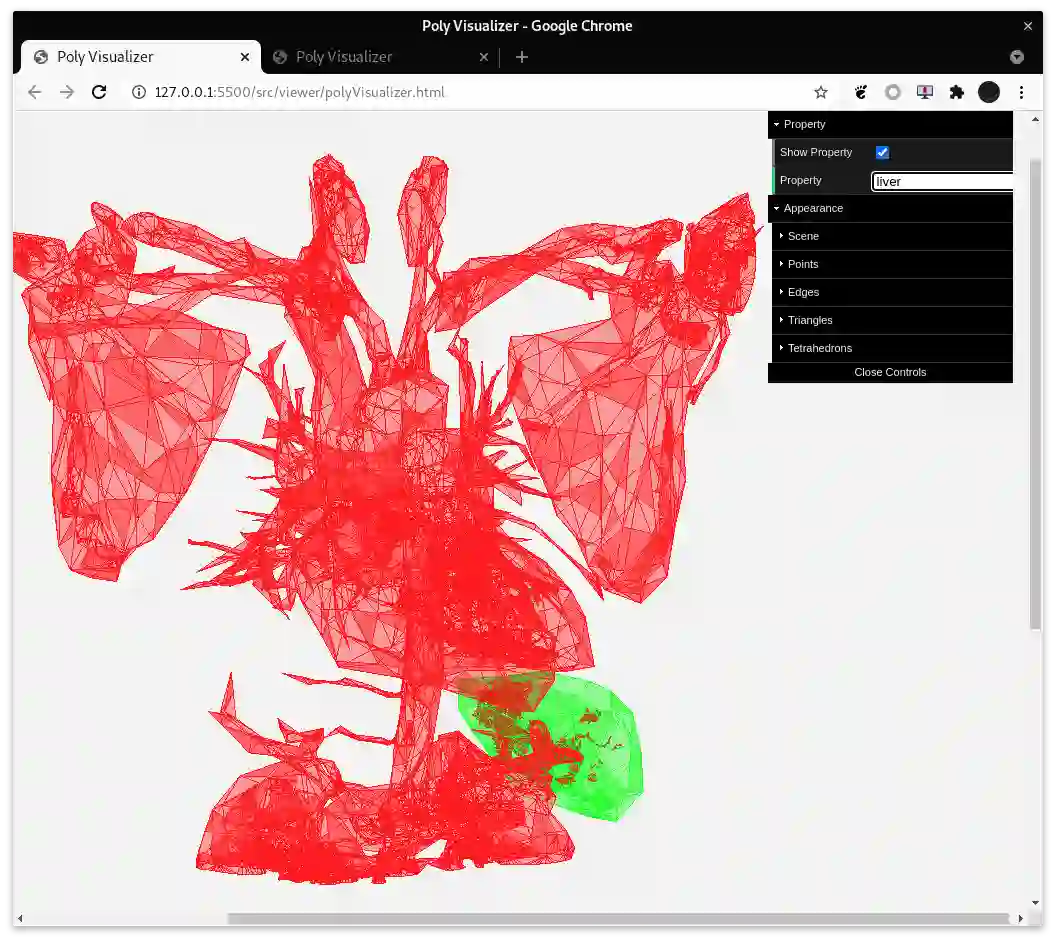
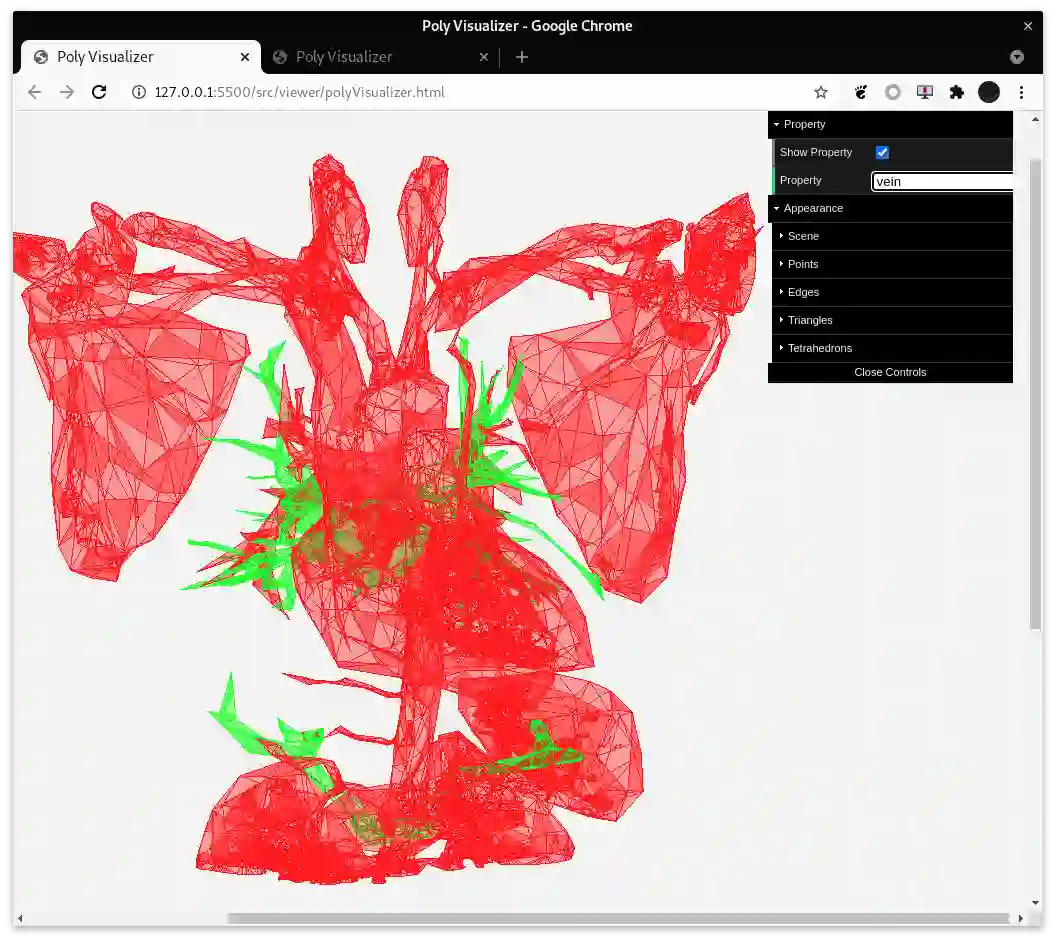
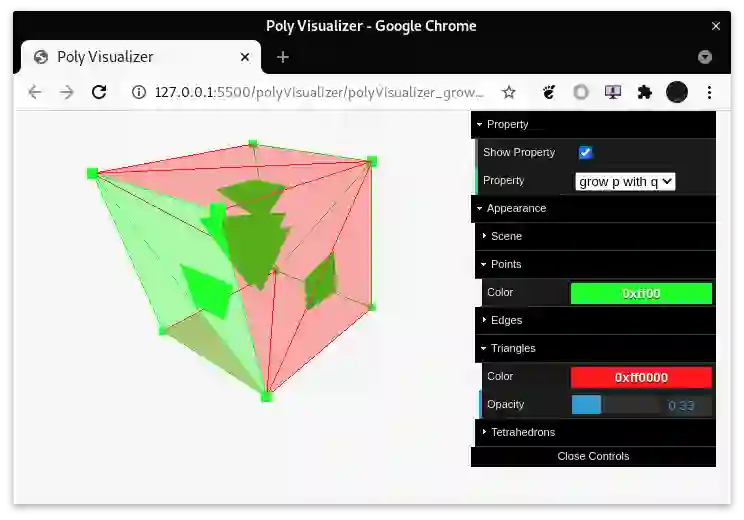
Topological Spatial Model Checking is a recent paradigm that combines Model Checking with the topological interpretation of Modal Logic. The Spatial Logic of Closure Spaces, SLCS, extends Modal Logic with reachability connectives that, in turn, can be used for expressing interesting spatial properties, such as "being near to" or "being surrounded by". SLCS constitutes the kernel of a solid logical framework for reasoning about discrete space, such as graphs and digital images, interpreted as quasi discrete closure spaces. In particular, the spatial model checker VoxLogicA, that uses an extended version of SLCS, has been used successfully in the domain of medical imaging. However, SLCS is not restricted to discrete space. Following a recently developed geometric semantics of Modal Logic, we show that it is possible to assign an interpretation to SLCS in continuous space, admitting a model checking procedure, by resorting to models based on polyhedra. In medical imaging such representations of space are increasingly relevant, due to recent developments of 3D scanning and visualisation techniques that exploit mesh processing. We demonstrate feasibility of our approach via a new tool, PolyLogicA, aimed at efficient verification of SLCS formulas on polyhedra, while inheriting some well-established optimization techniques already adopted in VoxLogicA. Finally, we cater for a geometric definition of bisimilarity, proving that it characterises logical equivalence.