A Power Method for Computing Singular Value Decomposition

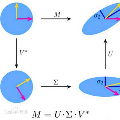
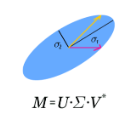
The singular value decomposition (SVD) allows to put a matrix as a product of three matrices: a matrix with the left singular vectors, a matrix with the positive-valued singular values and a matrix with the right singular vectors. There are two main approaches allowing to get the SVD result: the classical method and the randomized method. The analysis of the classical approach leads to accurate singular values. The randomized approach is especially used for high dimensional matrix and is based on the approximation accuracy without computing necessary all singular values. In this paper, the SVD computation is formalized as an optimization problem and a use of the gradient search algorithm. That results in a power method allowing to get all or the first largest singular values and their associated right vectors. In this iterative search, the accuracy on the singular values and the associated vector matrix depends on the user settings. Two applications of the SVD are the principal component analysis and the autoencoder used in the neural network models.