Robust optimal estimation of location from discretely sampled functional data

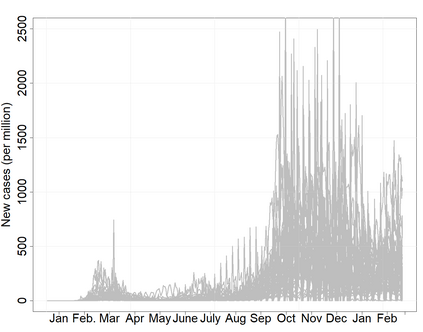
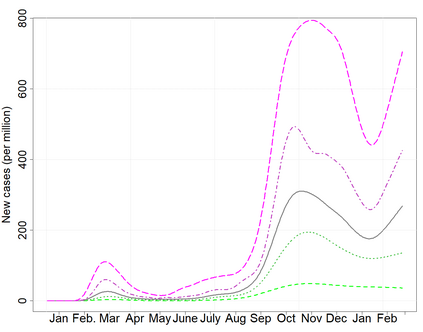
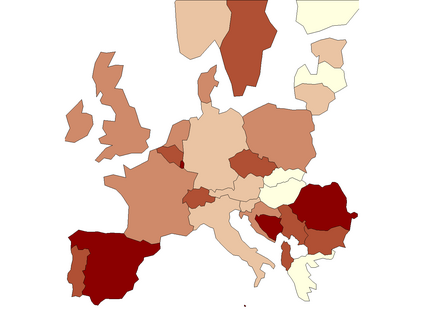
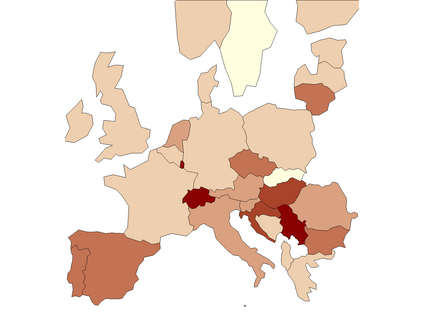
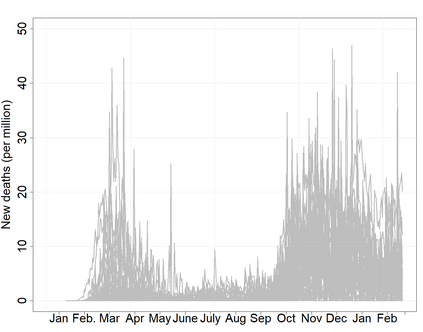
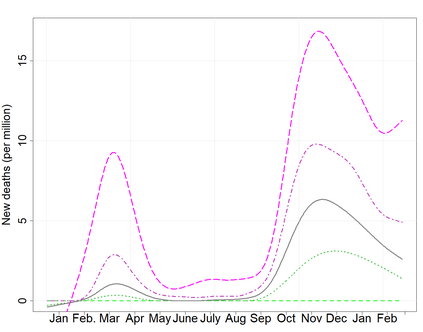
Estimating location is a central problem in functional data analysis, yet most current estimation procedures either unrealistically assume completely observed trajectories or lack robustness with respect to the many kinds of anomalies one can encounter in the functional setting. To remedy these deficiencies we introduce the first class of optimal robust location estimators based on discretely sampled functional data. The proposed method is based on M-type smoothing spline estimation with repeated measurements and is suitable for both commonly and independently observed trajectories that are subject to measurement error. We show that under suitable assumptions the proposed family of estimators is minimax rate optimal both for commonly and independently observed trajectories and we illustrate its highly competitive performance and practical usefulness in a Monte-Carlo study and a real-data example involving recent Covid-19 data.