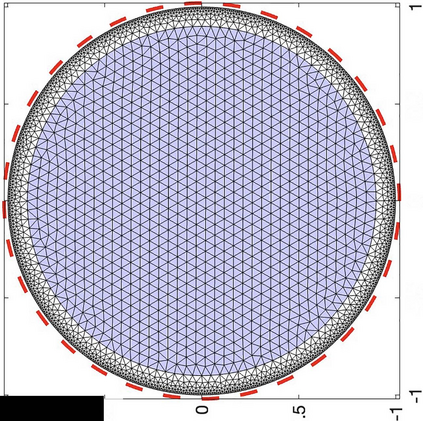
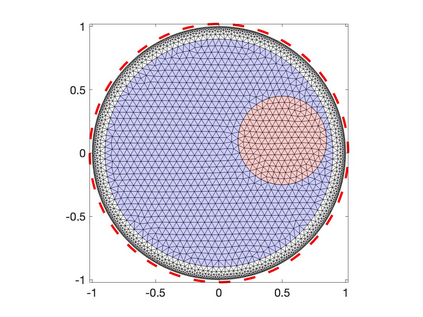
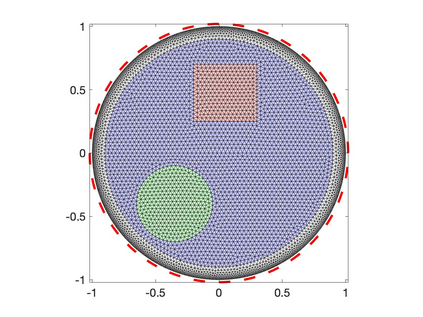
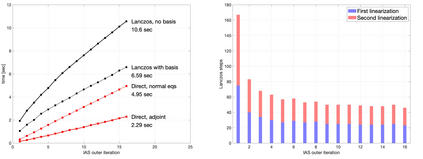
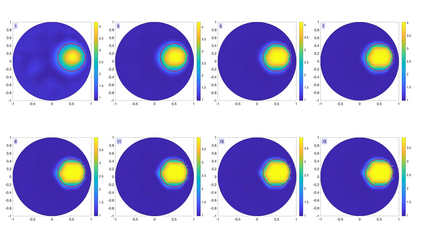
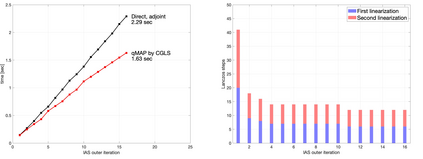
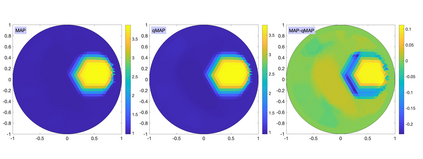
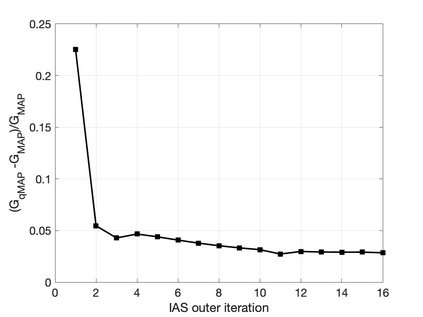
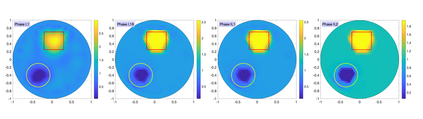
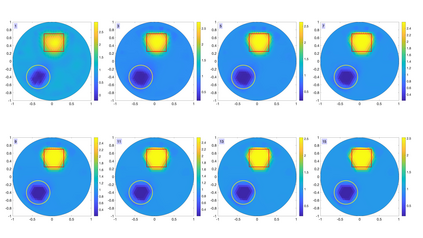
The electrical impedance tomography (EIT) problem of estimating the unknown conductivity distribution inside a domain from boundary current or voltage measurements requires the solution of a nonlinear inverse problem. Sparsity promoting hierarchical Bayesian models have been shown to be very effective in the recovery of almost piecewise constant solutions in linear inverse problems. We demonstrate that by exploiting linear algebraic considerations it is possible to organize the calculation for the Bayesian solution of the nonlinear EIT inverse problem via finite element methods with sparsity promoting priors in a computationally efficient manner. The proposed approach uses the Iterative Alternating Sequential (IAS) algorithm for the solution of the linearized problems. Within the IAS algorithm, a substantial reduction in computational complexity is attained by exploiting the low dimensionality of the data space and an adjoint formulation of the Tikhonov regularized solution that constitutes part of the iterative updating scheme. Numerical tests illustrate the computational efficiency of the proposed algorithm. The paper sheds light also on the convexity properties of the objective function of the maximum a posteriori (MAP) estimation problem.
翻译:暂无翻译