Partitioned Deep Learning of Fluid-Structure Interaction

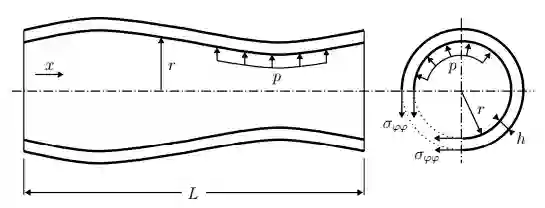
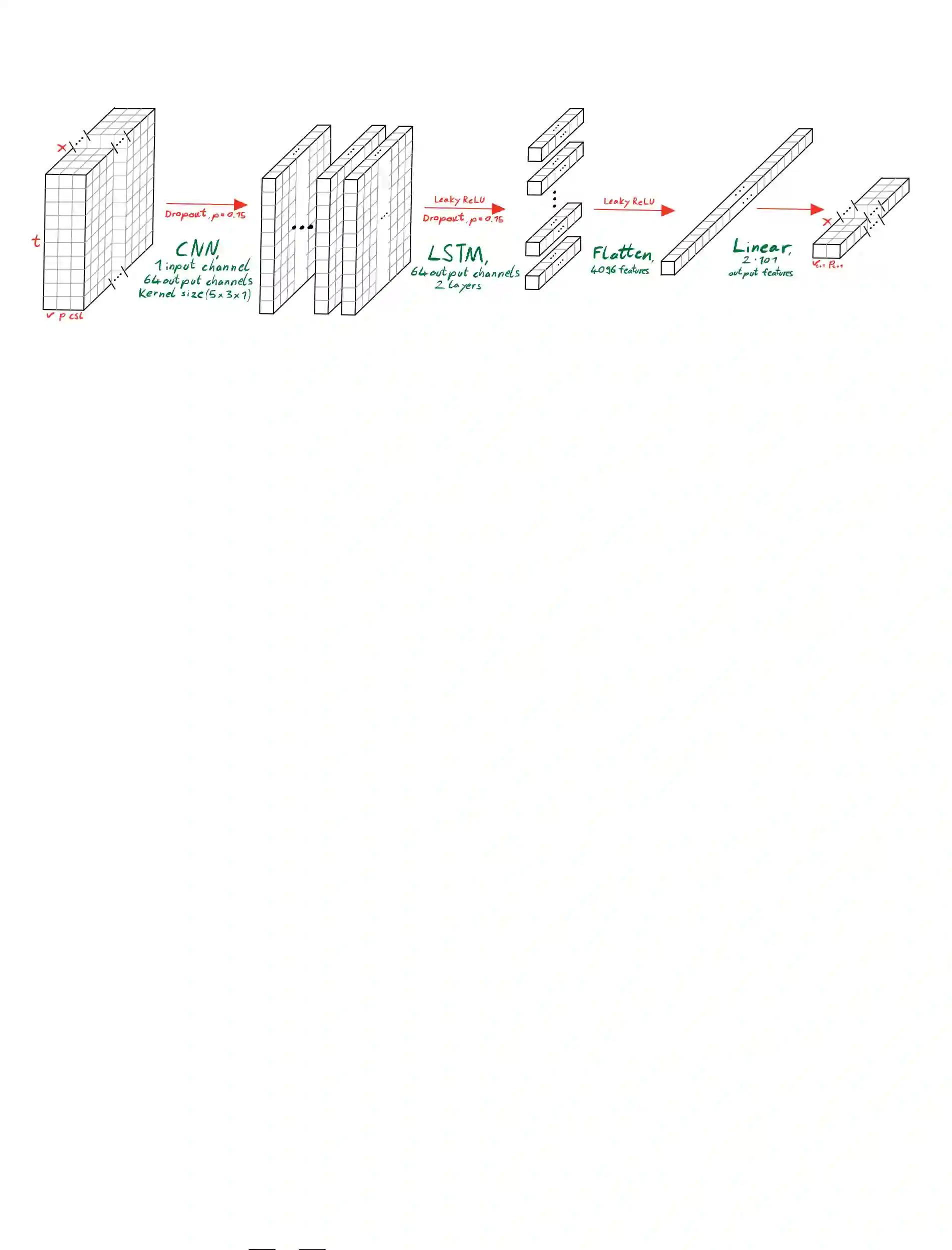
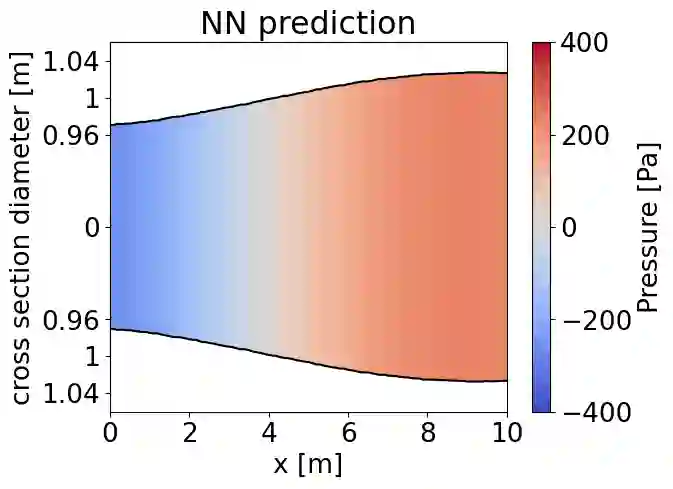
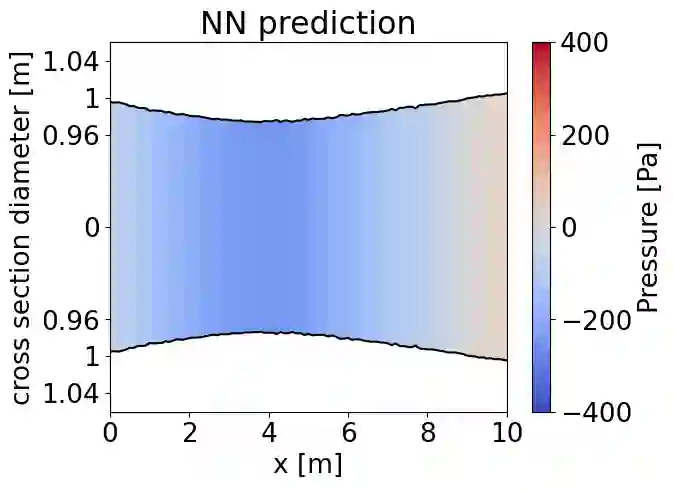
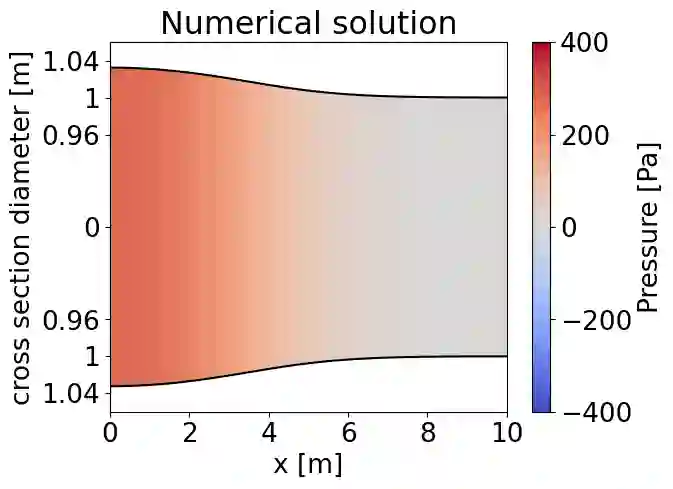
We present a partitioned neural network-based framework for learning of fluid-structure interaction (FSI) problems. We decompose the simulation domain into two smaller sub-domains, i.e., fluid and solid domains, and incorporate an independent neural network for each. A library is used to couple the two networks which takes care of boundary data communication, data mapping and equation coupling. Simulation data are used for training of the both neural networks. We use a combination of convolutional and recurrent neural networks (CNN and RNN) to account for both spatial and temporal connectivity. A quasi-Newton method is used to accelerate the FSI coupling convergence. We observe a very good agreement between the results of the presented framework and the classical numerical methods for simulation of 1d fluid flow inside an elastic tube. This work is a preliminary step for using neural networks to speed-up the FSI coupling convergence by providing an accurate initial guess in each time step for classical numerical solvers